Question

Answer 1

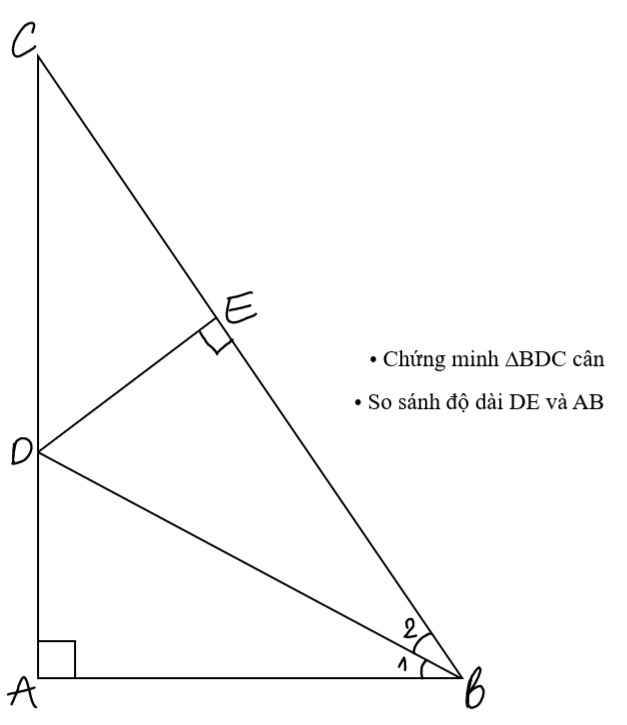
Bổ sung đề: \(\hat{ABC}=60^0\)

a: Ta có: BD là phân giác của góc ABC

=>\(\hat{ABD}=\hat{CBD}=\frac12\cdot\hat{ABC}=\frac12\cdot60^0=30^0\)

ΔABC vuông tại A

=>\(\hat{ABC}+\hat{ACB}=90^0\)

=>\(\hat{ACB}=90^0-60^0=30^0\)

Xét ΔDBC có \(\hat{DBC}=\hat{DCB}\left(=30^0\right)\)

nên ΔDBC cân tại D

b: Ta có: \(\hat{ADB}+\hat{ABD}=90^0\) (ΔABD vuông tại A)

=>\(\hat{ADB}=90^0-30^0=60^0\)

Xét ΔABD có \(\hat{ADB}>\hat{ABD}\)

mà AB,AD lần lượt là cạnh đối diện của các góc ADB,ABD

nên AB>AD

Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\hat{ABD}=\hat{EBD}\)

Do đó: ΔBAD=ΔBED

=>DA=DE

mà DA<AB

nên DE<AB