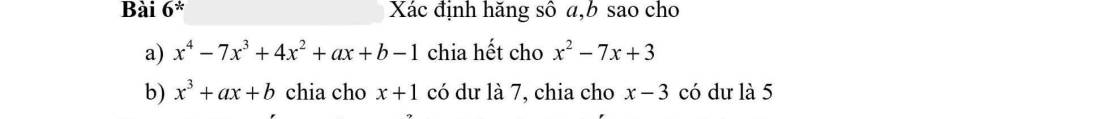6a) Đặt f(x) = x^4-7x^3+4x^2+ax+b-1
có f(x) chia hết cho x^2-7x+3 nên theo định lý bezout, ta có:
f(x) = (x^2-7x+3)(x^2+mx+n) (1)
Do hệ số của x^3 bằng - 7 và hệ số của x^3 đa thức (1) là (m-7) nên ta có m = 0
=> f(x) = (x^2-7x+3)(x^2+n)
tương tự như vậy với hệ số của x^2 là 4 và hệ số của x^2 trong đa thức (1) là (n+3) nên n = 1
Do đó đa thức f(x) là (x^2-7x+3)(x^2+1) hay f(x) = x^4 - 7x^3 + 4x^2 - 7x +3
Do đó ax + b - 1 = -7x + 3
=> a = -7; b = 4
b) Đặt x^3 + ax + b = (x+1)M(x) + 7 = (x-3)N(x) + 5
xét x = -1 => -1 - a + b =7; Xét x = 3 => 27 + 3a + b = 5
ta có hpt sau \(\left\{{}\begin{matrix}-a+b=8\\3a+b=-22\end{matrix}\right.\)
giải hệ trên bằng casio là có kqua nhé