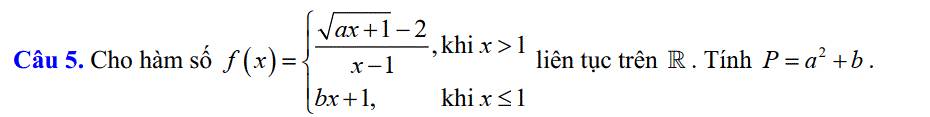Vì hàm số f(x) liên tục trên R
nên f(x) cũng sẽ liên tục khi x=1
=>\(\lim_{x\to1^{+}}f\left(x\right)=\lim_{x\to1^{+}}\frac{\sqrt{ax+1}-2}{x-1}\) sẽ có giá trị cụ thể và \(\lim_{x\to1^{-}}f\left(x\right)=\lim_{x\to1^{-}}bx+1=b\cdot1+1=b+1\) và \(\lim_{x\to1^{+}}f\left(x\right)=\lim_{x\to1^{-}}f\left(x\right)\)
=>\(\sqrt{ax+1}-2\) =0 khi x=1
=>\(\sqrt{a\cdot1+1}=2\)
=>a+1=4
=>a=3
=>\(\lim_{x\to1^{+}}f\left(x\right)=\lim_{x\to1^{+}}\frac{\sqrt{3x+1}-2}{x-1}\)
\(=\lim_{x\to1^{+}}\frac{3x+1-4}{\left(x-1\right)\left(\sqrt{3x+1}+2\right)}=\lim_{x\to1^{+}}\frac{3}{\sqrt{3x+1}+2}=\frac{3}{\sqrt{3\cdot1+1}+2}=\frac34\)
\(\lim_{x\to1^{+}}f\left(x\right)=\lim_{x\to1^{-}}f\left(x\right)\)
=>b+1=3/4
=>b=-1/4
\(P=a^2+b=3^2+\frac{-1}{4}=9-\frac14=\frac{35}{4}\)