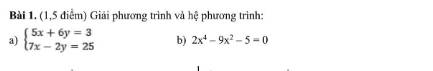\(a)\left\{{}\begin{matrix}5x+6y=3\\7x-2y=25\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}5x+6y=3\\21x-6y=75\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}26x=78\\5x+6y=3\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{78}{26}=3\\5\cdot3+6y=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\) là nghiệm của hệ phương trình
\(b)2x^4-9x^2-5=0\)
Đặt: `t=x^2`
\(\Rightarrow2t^2-9t-5=0\)
\(\Delta=b^2-4ac=\left(-9\right)^2-4\cdot2\cdot\left(-5\right)=121>0\)
`=>` Phương trình trên luôn có `2` nghiệm phân biệt
\(t_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-9\right)-\sqrt{121}}{2\cdot2}=-\dfrac{1}{2};\\ t_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-9\right)+\sqrt{121}}{2\cdot2}=5\)
Mà `t=x^2` `(**)`
`TH_1 .` Thay `t_1 =-1/2` vào `(**)`
`=> -1/2 = x^2`
`<=> x^2 = -1/2`
\(\Leftrightarrow\sqrt{x}=\sqrt{-\dfrac{1}{2}}\\ \Leftrightarrow\left|x\right|=-\dfrac{\sqrt{2}}{2}\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{2}}{2}\\x=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
`TH_2 .` Thay `t_2 = 5` vào `(**)`
`=> 5 = x^2`
`<=> x^2 = 5`
\(\Leftrightarrow\sqrt{x}=\sqrt{5}\\ \Leftrightarrow\left|x\right|=\sqrt{5}\\ \Leftrightarrow\left[{}\begin{matrix}x=\sqrt{5}\\x=-\sqrt{5}\end{matrix}\right.\)
Vậy, \(S=\left\{-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2};\sqrt{5};-\sqrt{5}\right\}.\)