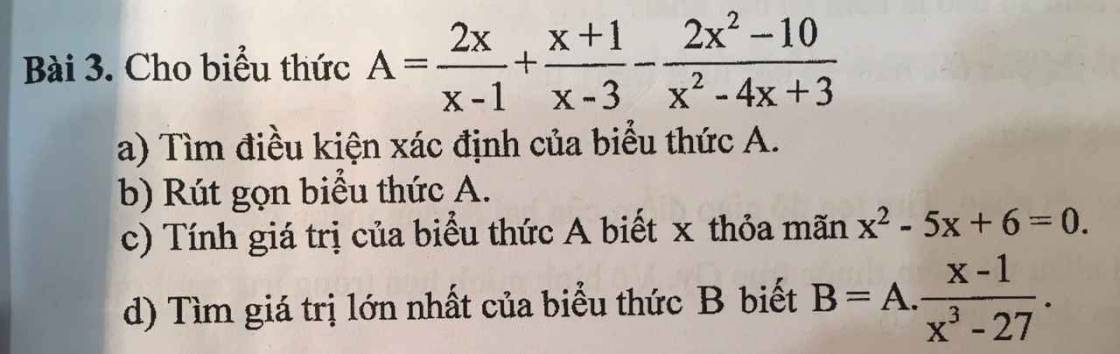a: ĐKXĐ: \(x\notin\left\{1;3\right\}\)
b: \(A=\dfrac{2x}{x-1}+\dfrac{x+1}{x-3}-\dfrac{2x^2-10}{x^2-4x+3}\)
\(=\dfrac{2x}{x-1}+\dfrac{x+1}{x-3}-\dfrac{2x^2-10}{\left(x-1\right)\left(x-3\right)}\)
\(=\dfrac{2x\left(x-3\right)+\left(x+1\right)\left(x-1\right)-2x^2+10}{\left(x-1\right)\left(x-3\right)}\)
\(=\dfrac{2x^2-6x+x^2-1-2x^2+10}{\left(x-1\right)\left(x-3\right)}=\dfrac{x^2-6x+9}{\left(x-1\right)\left(x-3\right)}\)
\(=\dfrac{\left(x-3\right)^2}{\left(x-1\right)\left(x-3\right)}=\dfrac{x-3}{x-1}\)
c: \(x^2-5x+6=0\)
=>(x-2)(x-3)=0
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
Thay x=2 vào A, ta được:
\(A=\dfrac{2-3}{2-1}=\dfrac{-1}{1}=-1\)
d: \(B=A\cdot\dfrac{x-1}{x^3-27}=\dfrac{x-3}{x-1}\cdot\dfrac{x-1}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{1}{x^2+3x+9}\)
\(=\dfrac{1}{x^2+3x+\dfrac{9}{4}+\dfrac{27}{4}}\)
\(=\dfrac{1}{\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}}< =1:\dfrac{27}{4}=\dfrac{4}{27}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(x+\dfrac{3}{2}=0\)
=>\(x=-\dfrac{3}{2}\)