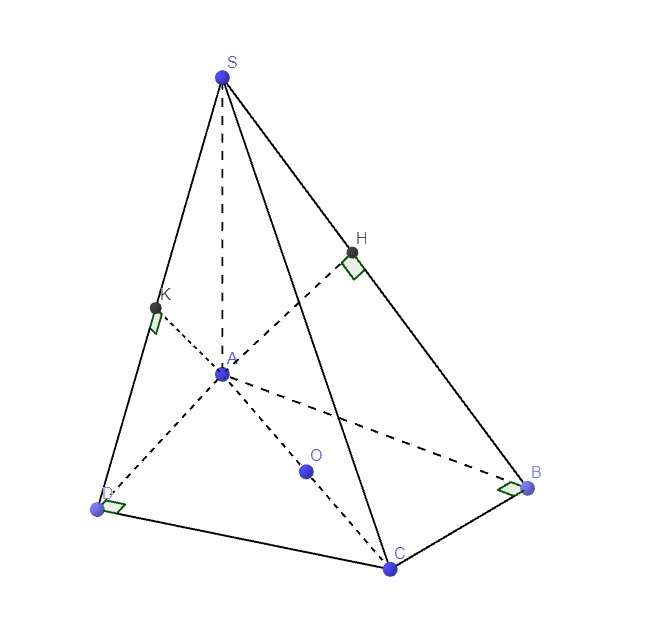
Ta có:
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (1) và \(SA\perp BC\) (2)
ABCD nội tiếp đường tròn đường kính AC \(\Rightarrow\widehat{ABC}=\widehat{ADC}=90^0\)
\(\Rightarrow AB\perp BC\) (3) và \(AD\perp CD\) (4)
Từ (2);(3) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (5)
Từ (1);(4) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AK\)
lại có \(AK\perp SD\left(gt\right)\Rightarrow AK\perp\left(SCD\right)\Rightarrow AK\perp SC\) (6)
(5);(6) \(\Rightarrow SC\perp\left(AHK\right)\)
b.
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\Rightarrow\Delta SAC\) vuông tại A
\(AC=\dfrac{AB}{sin\widehat{ACB}}=\dfrac{2\sqrt{3}}{3}AB\)
\(\Rightarrow tan\widehat{ASC}=\dfrac{AC}{SA}=\dfrac{AB\sqrt{3}}{\dfrac{2\sqrt{3}}{3}AB}=\dfrac{3}{2}\)
\(\Rightarrow\widehat{ASC}\approx56^019'\)