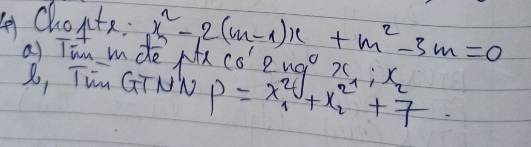Question

Answer 1

Lời giải:
a. Để pt có 2 nghiệm thì:

$\Delta'=(m-1)^2-(m^2-3m)\geq 0$

$\Leftrightarrow m+1\geq 0$

$\Leftrightarrow m\geq -1$

b.

Gọi $x_1,x_2$ là 2 nghiệm của pt. Áp dụng định lý Viet:

$x_1+x_2=2(m-1)$

$x_1x_2=m^2-3m$

Khi đó:

$P=x_1^2+x_2^2+7=(x_1+x_2)^2-2x_1x_2+7$

$=4(m-1)^2-2(m^2-3m)+7=2m^2-2m+11=2(m^2-m+\frac{1}{4})+10,5$

$=2(m-\frac{1}{2})^2+10,5\geq 10,5$

Vậy $P_{\min}=10,5$. Giá trị này đạt được khi $m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}$