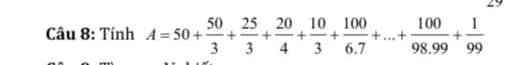Question

Answer 1

\(A=50+\dfrac{50}{3}+\dfrac{25}{3}+\dfrac{20}{4}+\dfrac{10}{3}+\dfrac{100}{6\cdot7}+...+\dfrac{100}{98\cdot99}+\dfrac{1}{99}\)

\(=\dfrac{100}{2}+\dfrac{100}{6}+\dfrac{100}{12}+...+\dfrac{100}{99\cdot100}\)

\(=100\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{99\cdot100}\right)\)

\(=100\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)

\(=100\left(1-\dfrac{1}{100}\right)=100\cdot\dfrac{99}{100}=99\)