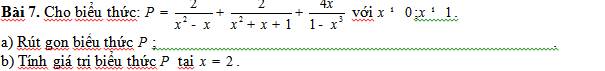a) \(P=\dfrac{2}{x^2-x}+\dfrac{2}{x^2+x+1}+\dfrac{4x}{1-x^3}\)
\(P=\dfrac{2}{x\left(x-1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{4x}{x^3-1}\)
\(P=\dfrac{2}{x\left(x-1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2\left(x^2+x+1\right)}{x\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2x\left(x-1\right)}{x\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{4x^2}{x\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2x^2+2x+2+2x^2-2x-4x^2}{x\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2}{x\left(x-1\right)\left(x^2+x+1\right)}\)
b) Thay `x=2` vào P ta có:
\(P=\dfrac{2}{2\cdot\left(2-1\right)\cdot\left(2^2+2+1\right)}=\dfrac{1}{7}\)