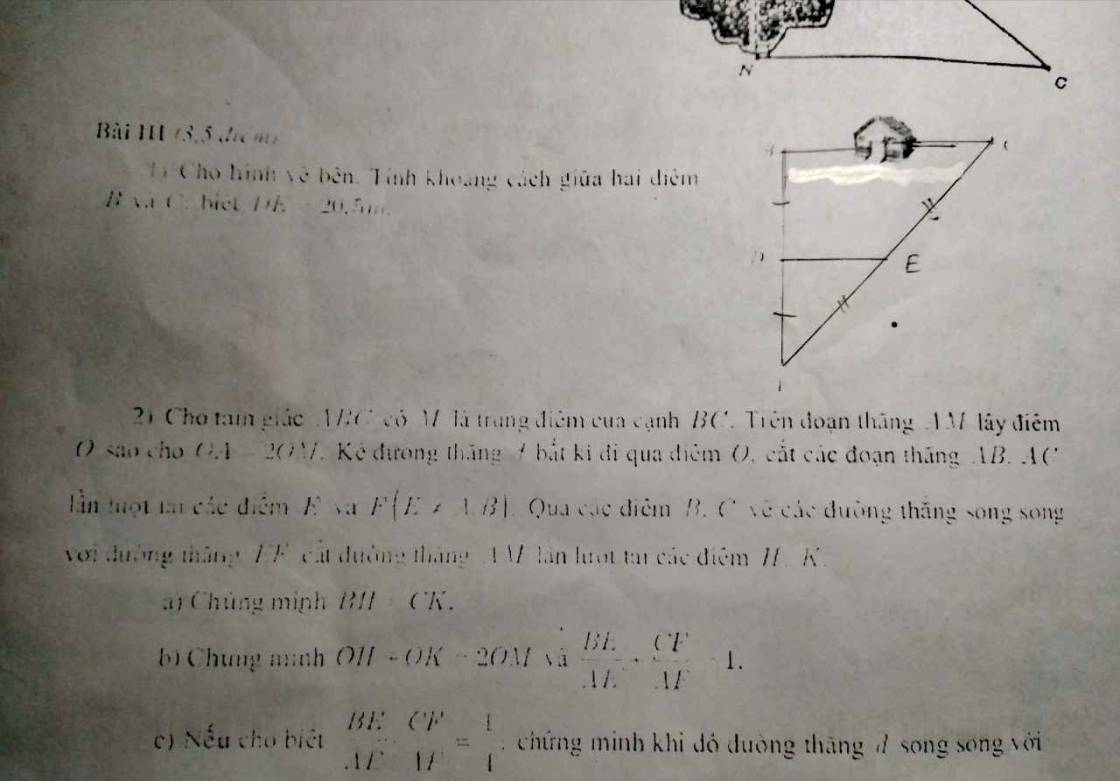8 tháng 2 lúc 8:02
1:
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và DE=BC/2
=>\(BC=2\cdot DE=2\cdot20,5=41\left(m\right)\)
2:
a: Xét ΔBHM và ΔCKM có
\(\widehat{HMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
\(\widehat{MBH}=\widehat{MCK}\)(hai góc so le trong, BH//CK)
Do đó; ΔBHM=ΔCKM
=>BH=CK
b: ta có: ΔBHM=ΔCKM
=>HM=KM
mà M nằm giữa H và K
nên M là trung điểm của HK
OH+OK
=OH+OH+HK
=2OH+2HM
=2(OH+HM)
=2OM
Đúng 2
Bình luận (0)
