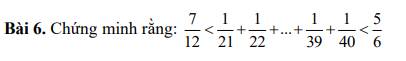Đặt \(S=\dfrac{1}{21}+...+\dfrac{1}{40}\)
\(S=\left(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{30}\right)+\left(\dfrac{1}{31}+...+\dfrac{1}{40}\right)\)
\(S>\left(\dfrac{1}{30}+\dfrac{1}{30}+...+\dfrac{1}{30}\right)+\left(\dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}\right)=\dfrac{10}{30}+\dfrac{10}{40}=\dfrac{7}{12}\)
\(S< \left(\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\right)+\left(\dfrac{1}{30}+\dfrac{1}{30}+...+\dfrac{1}{30}\right)=\dfrac{10}{20}+\dfrac{10}{30}=\dfrac{5}{6}\)
\(\Rightarrow\dfrac{7}{12}< S< \dfrac{5}{6}\)
Ta có : \(\dfrac{1}{21}+\dfrac{1}{32}+...+\dfrac{1}{39}+\dfrac{1}{40}>\dfrac{10}{40}=\dfrac{1}{3}\)
\(và\) \(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}>\dfrac{10}{40}=\dfrac{1}{4}\)
→\(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{39}+\dfrac{1}{40}>\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)
Ta có : \(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{29}+\dfrac{1}{30}< \dfrac{10}{20}=\dfrac{1}{2}\)
và\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{39}+\dfrac{1}{40}< \dfrac{10}{30}=\dfrac{1}{3}\)
→\(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{39}+\dfrac{1}{40}< \dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}\)
\(\dfrac{7}{12}< \dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{39}+\dfrac{1}{40}< \dfrac{5}{6}\)