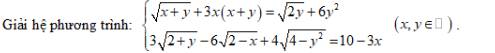ĐKXĐ:
Từ pt đầu:
\(\sqrt{x+y}-\sqrt{2y}+3\left(x^2+xy-2y^2\right)=0\)
\(\Leftrightarrow\dfrac{x-y}{\sqrt{x+y}+\sqrt{2y}}+3\left(x-y\right)\left(x+2y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(\dfrac{1}{\sqrt{x+y}+\sqrt{2y}}+3\left(x+2y\right)\right)=0\)
\(\Leftrightarrow x-y=0\Rightarrow y=x\)
Thay xuống pt dưới:
\(3\sqrt{2+x}-6\sqrt{2-x}+4\sqrt{4-x^2}=10-3x\)
Đặt \(\left\{{}\begin{matrix}\sqrt{2+x}=a\ge0\\\sqrt{2-x}=b\ge0\end{matrix}\right.\) \(\Rightarrow10-3x=a^2+4b^2\)
Pt trở thành:
\(3a-6b+4ab=a^2+4b^2\)
\(\Leftrightarrow\left(a-2b\right)^2-3\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(a-2b-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2b\\a=2b+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}=2\sqrt{2-x}\\\sqrt{2+x}=2\sqrt{2-x}+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=4\left(2-x\right)\\2+x=4\left(2-x\right)+9+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\\12\sqrt{2-x}=5x-15\left(1\right)\end{matrix}\right.\)
Do \(x\le2\) để căn thức có nghĩa nên \(5x-15< 0\Rightarrow\) (1) vô nghiệm
\(\Rightarrow x=y=\dfrac{6}{5}\) là nghiệm của hệ