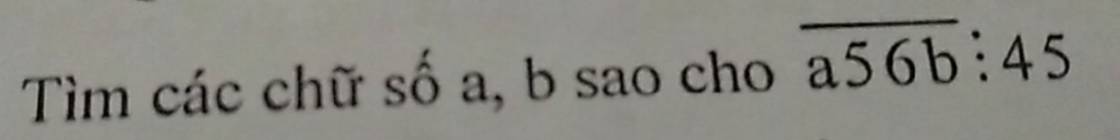Đặt \(X=\overline{a56b}\)
Để X chia hết cho 45 thì X chia hết cho 9 và X chia hết cho 5
Để X chia hết cho 5 thì b=0 hoặc b=5
TH1: b=0
=>\(X=\overline{a560}\)
X chia hết cho 9
=>\(a+5+6+0⋮9\)
=>\(a+11⋮9\)
=>a=7
TH2: b=5
=>\(X=\overline{a565}\)
X chia hết cho 9
=>\(a+5+6+5⋮9\)
=>\(a+16⋮9\)
=>a=2
Do \(45⋮\left\{5;9\right\}\Rightarrow\overline{a56b}⋮5\) và \(\overline{a56b}⋮9\)
\(\Rightarrow b=0\) hoặc \(b=5\)
- Nếu \(b=0\Rightarrow a+5+6⋮9\Rightarrow a+11⋮9\)
Mà \(1\le a\le9\Rightarrow12\le a+11\le20\)
\(\Rightarrow a+11=18\)
\(\Rightarrow a=7\)
\(\Rightarrow\) Số đó là \(7560\)
- Nếu \(b=5\Rightarrow a+5+6+5⋮9\)
\(\Rightarrow a+16⋮9\)
Do \(17\le a+16\le25\Rightarrow a+16=18\)
\(\Rightarrow a=2\)
\(\Rightarrow\) Số đó là \(2565\)
Vậy \(a=7;b=0\) hoặc \(a=2;b=5\)
Vì 45=9 x 5=>a56b phải chia hết cho 5 và 9
Để a56b chia hết cho 5 thì b phải =0 hoặc =5
Nếu b=5 ta có số:a565
Để a565 chia hết cho 9 ta có:(a+5+6+5) chia hết cho 9
a+16 chia hết cho 9
=> a=3.Vậy ta có số 3565
Nếu b=0 ta có sô a560
Để a560 chia hết cho 9 thì:(a+5+6+0) chia hết cho 9
a+11 chia hết cho 9
=>a=7.Vậy ta có số cần tìm là 7560
Vậy ta có 2 số cần tìm là:3565 và 7560
THAM KHẢO