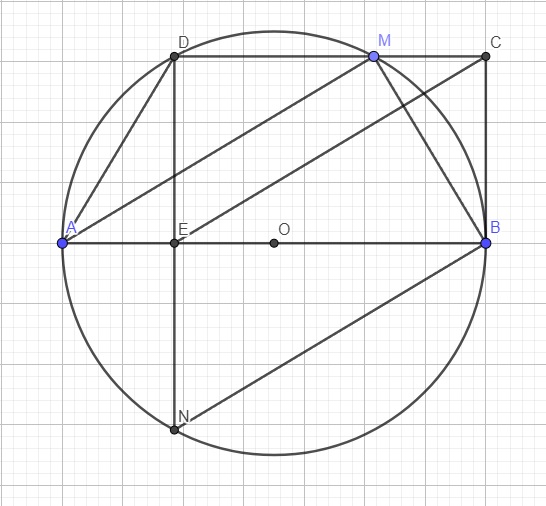
a.
Do \(AM||BN\Rightarrow AN=BM\) (hai dây song song chắn 2 cung bằng nhau)
Do \(DM||AB\Rightarrow AD=BM\) (hai dây song song chắn 2 cung bằng nhau)
\(\Rightarrow AN=AD\)
Lại có \(ON=OD=R\)
\(\Rightarrow AO\) là trung trực của DN
\(\Rightarrow AO\perp DN\) hay \(AB\perp DN\) tại E
b.
Do \(AN=BM\Rightarrow\widehat{ADN}=\widehat{BAM}\)
Mà \(\left\{{}\begin{matrix}\widehat{ADN}+\widehat{DAB}=90^0\\\widehat{BAM}+\widehat{ABM}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{DAB}=\widehat{ABM}\)
Lại có \(\widehat{BMC}=\widehat{AMB}\) (so le trong)
\(\Rightarrow\widehat{DAB}=\widehat{BMC}\)
Tứ giác AECM có 2 cặp cạnh đối song song nên AECM là hình bình hành
\(\Rightarrow AE=MC\)
Xét hai tam giác AED và MCB có:
\(\left\{{}\begin{matrix}AD=BM\left(cmt\right)\\\widehat{DAE}=\widehat{BMC}\left(cmt\right)\\AE=MC\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED=\Delta MCB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ADE}=\widehat{MBC}\)
\(\Rightarrow\widehat{MBC}+\widehat{ABM}=\widehat{ADE}+\widehat{ABM}=\widehat{ADE}+\widehat{DAB}=90^0\)
\(\Rightarrow\widehat{ABC}=90^0\)
\(\Rightarrow BC\perp AB\)
\(\Rightarrow BC\) là tiếp tuyến của (O)