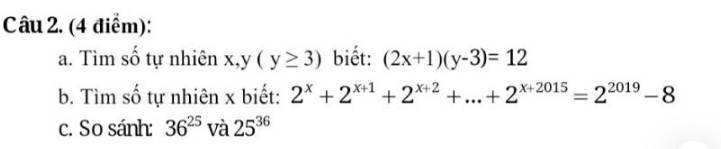a: (2x+1)(y-3)=12
mà 2x+1 lẻ và y-3>=0(do x,y là các số tự nhiên)
nên \(\left(2x+1\right)\left(y-3\right)=1\cdot12=3\cdot4\)
=>\(\left(2x+1;y-3\right)\in\left\{\left(1;12\right);\left(3;4\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(0;15\right);\left(1;7\right)\right\}\)
b: \(2^x+2^{x+1}+2^{x+2}+...+2^{x+2015}=2^{2019}-8\)
=>\(2^x+2^x\cdot2+2^x\cdot4+...+2^x\cdot2^{2015}=2^{2019}-8\)
=>\(2^x\left(1+2+2^2+...+2^{2015}\right)=8\left(2^{2016}-1\right)\)(1)
Đặt \(A=1+2+2^2+...+2^{2015}\)
=>\(2\cdot A=2+2^2+2^3+...+2^{2016}\)
=>\(2A-A=2+2^2+...+2^{2016}-1-2-...-2^{2015}\)
=>\(A=2^{2016}-1\)
Phương trình (1) sẽ tương đương với:
\(2^x\left(2^{2016}-1\right)=8\cdot\left(2^{2016}-1\right)\)
=>\(2^x=8=2^3\)
=>x=3
c: \(36^{25}=\left(6^2\right)^{25}=6^{50}\)
\(25^{36}=\left(5^2\right)^{36}=5^{72}\)
\(6^5< 5^7\left(7776< 78125\right)\)
=>\(6^{50}< 5^{70}\)
=>\(6^{50}< 5^{72}\)
=>\(36^{25}< 25^{36}\)