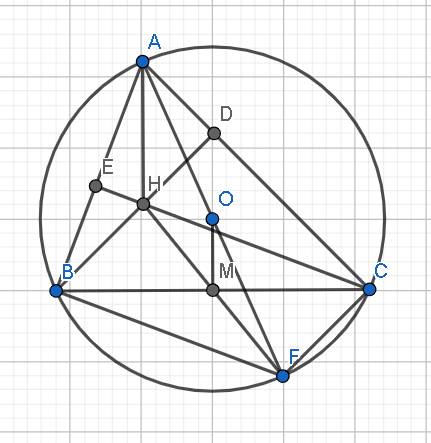
Bài 6
a) Ta có CE là đường cao của tam giác ABC
\(\Rightarrow CE\perp AB\) (1)
Xét đường tròn tâm O đường kính AF có B thuộc đường tròn, B không trùng với A và F
\(\Rightarrow\widehat{ABF}=90^o\) hay \(FB\perp AB\) (2)
Từ (1) và (2) CE//FB hay CH//FB
Chứng minh tương tự: BH // CF
=> Tứ giác BFHC là hình bình hành
b) Tứ giác BFHC là hình bình hành
=> BC và HF cắt nhau tại trung điểm mỗi đường
mà M là trung điểm của BC => HF đi qua M hay 3 điểm H, M, F thẳng hàng (đpcm)
c) Xét đường tròn tâm O có BC là dây cung khác đường kính, M là trung điểm cùa BC
=> \(OM\perp BC\) (3)
Xét tam giác ABC có hai đường cao BD, CE cắt nhau tại H
=> AH \(\perp\) BC(4)
Từ (3) và (4) : OM // AH
Xét tam giác FAH có OM // AH
=> \(\dfrac{FO}{FA}=\dfrac{FM}{FH}=\dfrac{OM}{AH}\)
Mà \(FO=\dfrac{1}{2}FA\)
=> \(\dfrac{FO}{FA}=\dfrac{1}{2}\Rightarrow\dfrac{OM}{AH}=\dfrac{1}{2}\)
hay \(OM=\dfrac{1}{2}AH\)(đpcm)