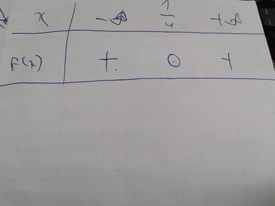1: Đặt f(x)=0
=>\(2x^2-3x+1=0\)
=>\(2x^2-2x-x+1=0\)
=>(x-1)(2x-1)=0
=>\(\left[{}\begin{matrix}x-1=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
Bảng xét dấu:
2:
Đặt f(x)=0
=>\(-x^2+4x+5=0\)
=>\(x^2-4x-5=0\)
=>(x-5)(x+1)=0
=>\(\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
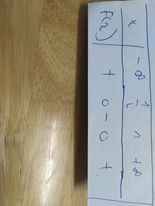
Bảng xét dấu:

3: Đặt \(f\left(x\right)=0\)
=>\(-3x^2+12x-12=0\)
=>\(-3\left(x^2-4x+4\right)=0\)
=>\(x^2-4x+4=0\)
=>\(\left(x-2\right)^2=0\)
=>x-2=0
=>x=2
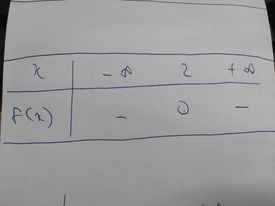
Bảng xét dấu:
4: Đặt f(x)=0
=>\(2x^2+2x+1=0\)
\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)
=>f(x)=0 vô nghiệm
=>f(x) luôn cùng dấu với a
mà a>0
nên f(x)>0 với mọi x
Bảng xét dấu:

5:
Đặt f(x)=0
=>\(4x^2-2x+\dfrac{1}{4}=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot4\cdot\dfrac{1}{4}=4-4=0\)
Vì Δ=0 nên phương trình có nghiệm kép là \(x=\dfrac{-b}{2a}=\dfrac{-\left(-2\right)}{2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)
Bảng xét dấu: