Question

Answer 1

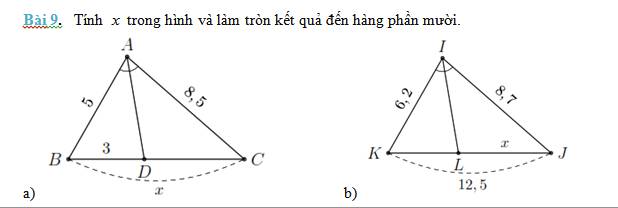
a: Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DC}{8,5}=\dfrac{3}{5}\)

=>\(DC=8,5\cdot\dfrac{3}{5}=5,1\)

BC=BD+DC

=5,1+3

=8,1

=>x=8,1

b: Xét ΔIKJ có IL là phân giác

nên \(\dfrac{LK}{KI}=\dfrac{LJ}{JI}\)

=>\(\dfrac{LK}{6,2}=\dfrac{LJ}{8,7}\)

mà LK+LJ=12,5

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{KL}{6,2}=\dfrac{LJ}{8,7}=\dfrac{KL+LJ}{6,2+8,7}=\dfrac{12.5}{14.9}=\dfrac{125}{149}\)

=>\(\dfrac{LJ}{8,7}=\dfrac{125}{149}\)

=>\(x=\dfrac{125}{149}\cdot8,7\simeq7,3\)