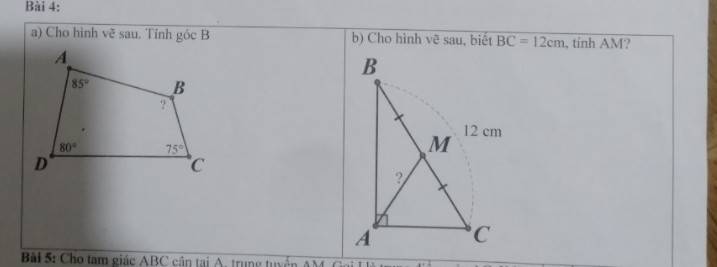
a) Xét tứ giác \(ABCD\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}\) (theo định lí tổng các góc trong tứ giác)
\(\Rightarrow 85^{\circ}+\widehat{B}+75^{\circ}+80^{\circ}=360^\circ\)
\(\Rightarrow\widehat{B}=360^{\circ}-\left(85^{\circ}+75^{\circ}+80^{\circ}\right)=120^{\circ}\)
b) Xét \(\Delta ABC\) vuông tại \(A\) có:
\(M\) là trung điểm của \(BC\)
\(\Rightarrow AM\) là đường trung tuyến ứng với cạnh huyền \(BC\)
\(\Rightarrow AM=\dfrac{1}{2}BC\) (t/c)
\(\Rightarrow AM=\dfrac{1}{2}\cdot12=6\left(cm\right)\)
Đúng 2
Bình luận (0)
