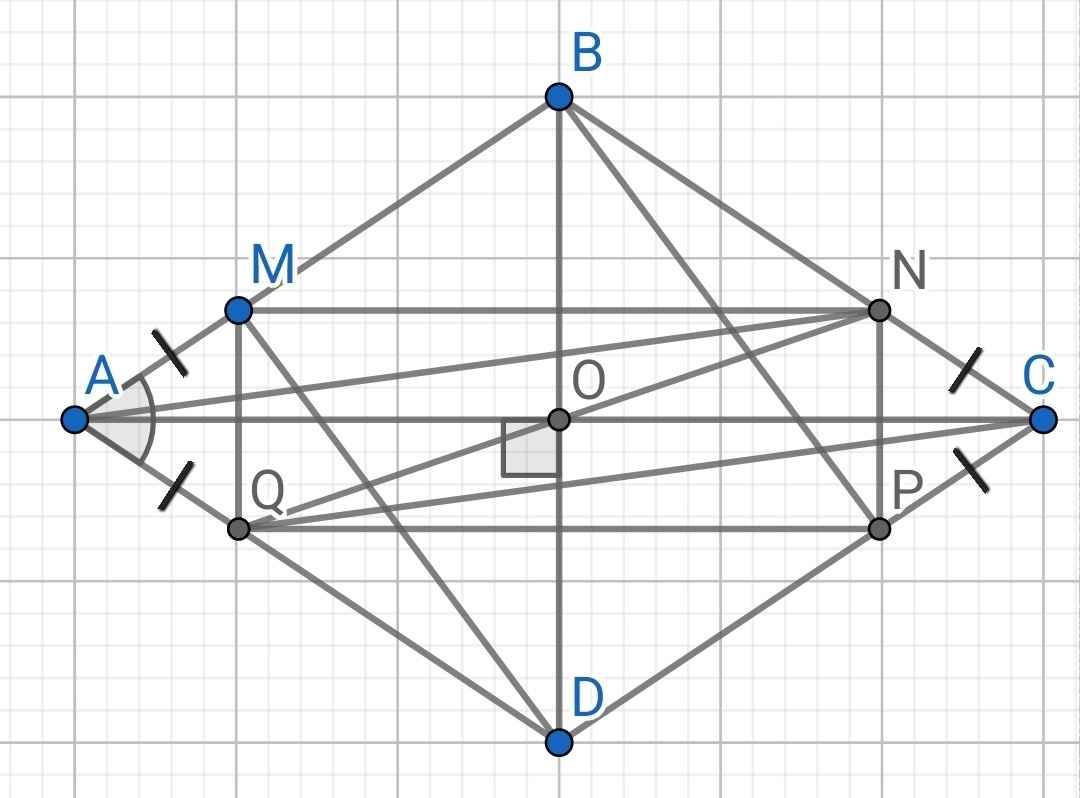
 a) ABCD là hình thoi
a) ABCD là hình thoi
⇒ AB = BC = CD = DA
Mà AM = CN
⇒ AB - AM = CD - CP
⇒ BM = PD
Lại có:
AB // CD (ABCD là hình thoi)
⇒ BM // PD
Tứ giác BMDP có:
BM // PD (cmt)
BM = PD (cmt)
⇒ BMDP là hình bình hành
b) Do O là giao điểm của hai đường chéo của hình thoi ABCD (gt)
⇒ O là trung điểm của AC
Do ABCD là hình thoi
⇒ AD // BC
⇒ AQ // CN
Tứ giác AQCN có:
AQ // CN (cmt)
AQ = CN (gt)
⇒ AQCN là hình bình hành
Mà O là trung điểm của AC
⇒ O là trung điểm của QN
⇒ Vậy N, O, Q thẳng hàng
c) Do ABCD là hình thoi
⇒ AC là tia phân giác của ∠BAD
⇒ AC là tia phân giác của ∠MAQ
∆AMQ có:
AM = AQ (gt)
⇒ ∆AMQ cân tại A
Mà AC là tia phân giác của ∠MAQ
⇒ AC cũng là đường trung trực của ∆MAQ
⇒ MQ ⊥ AC (1)
Do ABCD là hình thoi
⇒ AC ⊥ BD (2)
Từ (1) và (2) ⇒ MQ // BD (3)
Do ABCD là hình thoi
⇒ CA là tia phân giác của ∠BCD
⇒ CA là tia phân giác của ∠PCN
∆CPN có:
CP = CN (gt)
⇒ ∆CPN cân tại C
Mà CA là tia phân giác của ∠PCN (cmt)
⇒ CA cũng là đường trung trực của ∆PCN
⇒ CA ⊥ PN
Mà CA ⊥ BD (cmt)
⇒ PN // BD (4)
Từ (3) và (4) ⇒ MQ // PN
Do ABCD là hình thoi (gt)
⇒ ∠BAD = ∠BCD
⇒ ∠MAQ = ∠PCN
Xét ∆AMQ và ∆CPN có:
AM = CP (gt)
∠MAQ = ∠PCN (cmt)
AQ = CN (gt)
⇒ ∆AMQ = ∆CPN (c-g-c)
⇒ MQ = PN
Do AB = BC (cmt)
AM = CN (gt)
⇒ AB - AM = BC - CN
⇒ BM = BN
⇒ ∆BMN cân tại B
⇒ ∠BMN = (180⁰ - ∠MBN) : 2
Do AB = BC (cmt)
⇒ ∆ABC cân tại B
⇒ ∠BAC = (180⁰ - ∠ABC) : 2
Mà ∠ABC = ∠MBN
⇒ ∠BMN = ∠BAC
Mà ∠BMN và ∠BAC đồng vị
⇒ MN // AC
Mà AC ⊥ PN
⇒ MN ⊥ PN
⇒ ∠MNP = 90⁰
Tứ giác MNPQ có:
MQ // PN (cmt)
MQ = PN (cmt)
⇒ MNPQ là hình bình hành
Mà ∠MNP = 90⁰
⇒ MNPQ là hình chữ nhật
















