Lời giải:
Ta thấy:
Hai góc hiển thị $120^0$ và $60^0$ trong hình là 2 góc trong cùng phía. Mà tổng của chúng là $120^0+60^0=180^0$ nên $AB\parallel CD$
Xét tam giác $AOB$ và $DOC$ có:
$AB=CD$ (gt)
$\widehat{OAB}=\widehat{ODC}$ (so le trong)
$\widehat{OBA}=\widehat{OCD}$ (so le trong)
$\Rightarrow \triangle AOB=\triangle DOC$ (g.c.g)
$\Rightarrow OA=DO, OB=OC$
$\Rightarrow O$ là trung điểm của $AD, BC$ (đpcm)
Trắc nghiệm
Câu 1. Không câu nào đúng
Câu 2. C
Câu 3. D
Câu 4. C
Câu 5. B và D đúng
Phần tự luận
Bài 1
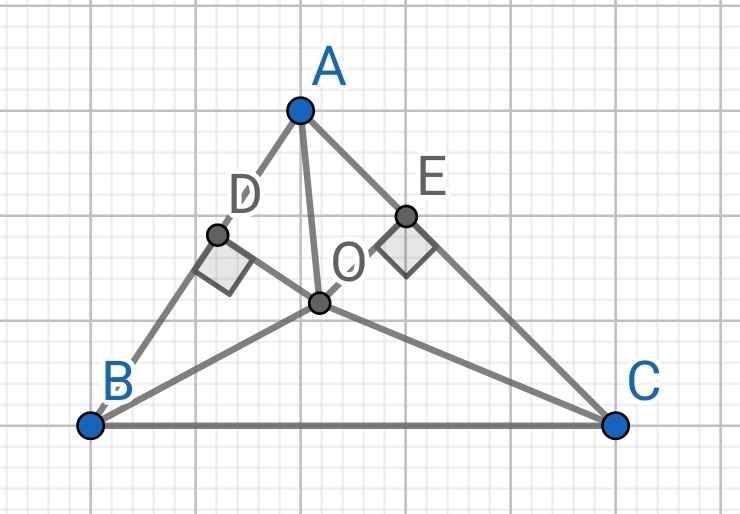Do O là giao điểm của hai đường phân giác của ∆ABC
⇒ AO là đường phân giác của BAC
⇒ ∠OAD = ∠OAE
Xét hai tam giác vuông: ∆AOD và ∆AOE có:
AO là cạnh chung
∠OAD = ∠OAE (cmt)
⇒ ∆AOD = ∆AOE (cạnh huyền - góc nhọn)
⇒ OD = OE (hai cạnh tương ứng)
Phần tự luận
Bài 2
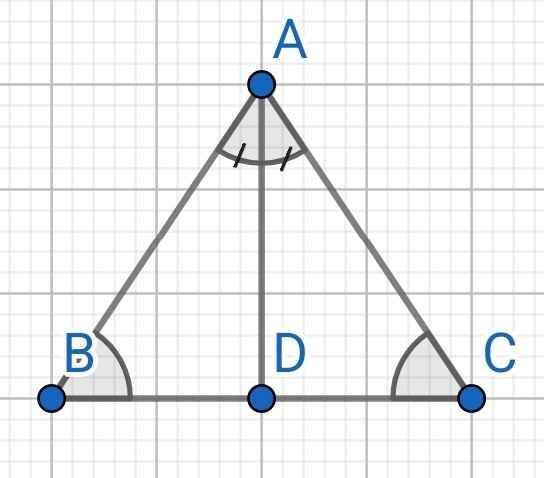Do AD là tia phân giác của BAC (gt)
⇒ ∠BAD = ∠CAD
∆ABC có:
∠B = ∠C (gt)
⇒ ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
∠BAD = ∠CAD (cmt)
AB = AC (cmt)
∠B = ∠C (gt)
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD (hai cạnh tương ứng)
Phần tự luận
Bài 3
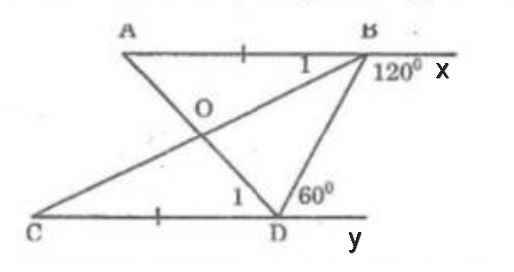Ta có:
∠BDC + ∠BDy = 180⁰ (kề bù)
⇒ ∠BDC = 180⁰ - ∠BDy
= 180⁰ - 60⁰
= 120⁰
⇒ ∠BDC = ∠CDx = 120⁰
Mà ∠BDC và ∠CDx là hai góc so le trong
⇒ AB // CD
⇒ ∠OBA = ∠OCD (so le trong)
∠OAB = ∠ODC (so le trong)
Xét ∆OAB và ∆ODC có:
∠OAB = ∠ODC (cmt)
AB = CD (gt)
∠OBA = ∠OCD (cmt)
⇒ ∆OAB = ∆ODC (c-g-c)
⇒ OA = OD (hai cạnh tương ứng)
⇒ O là trung điểm của AD
Do ∆OAB = ∆ODC (cmt)
⇒ OB = OC (hai cạnh tương ứng)
⇒ O là trung điểm của BC
