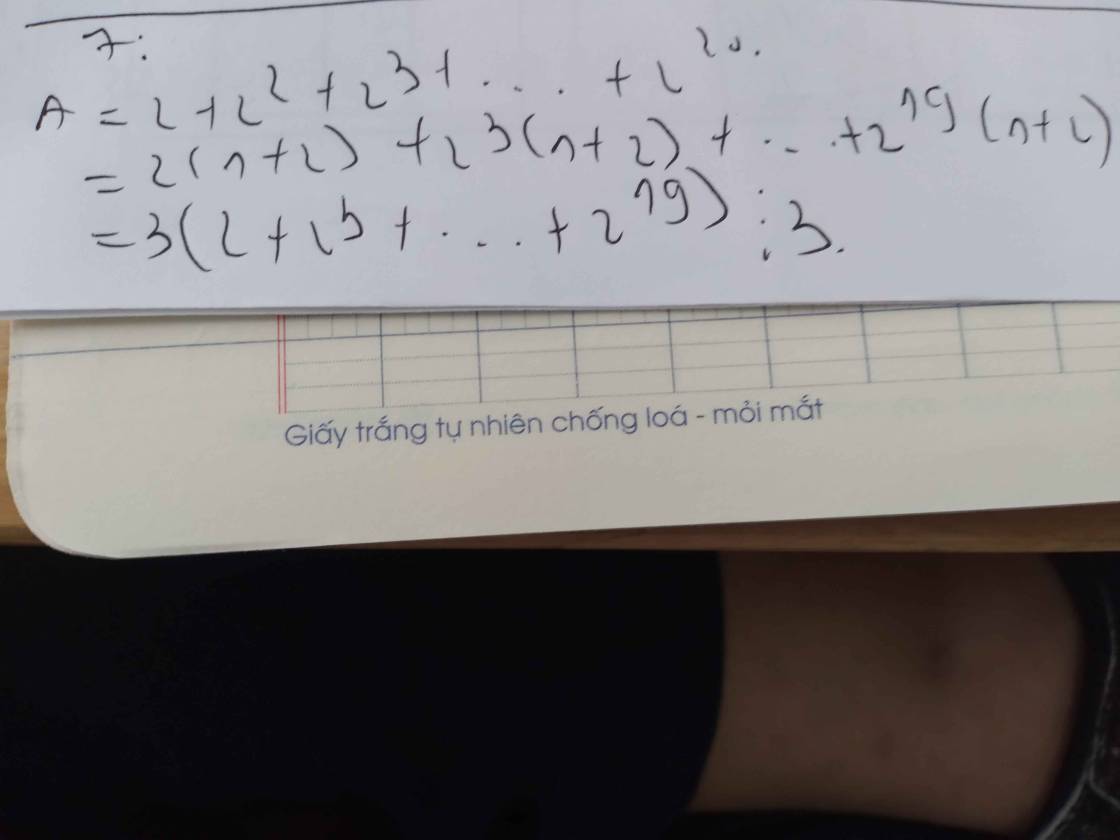`#3107.101107`
`6,`
`5^200` và `3^250`
Ta có:
`5^200 = 5^(4*50) = (5^4)^50 = 625^50`
`3^250 = 3^(5*50) = (3^5)^50 = 243^50`
Vì `625 > 243 => 625^50 > 243^50 => 5^200 > 3^250`
Vậy, `5^200 > 3^250`
`b)`
`3333^4444` và `4444^3333`
Ta có:
`3333^4444 = (3*1111)^(4*1111) = (3^4 * 1111^4)^1111 = 81^1111 * 1111^4444`
`4444^3333 = (4*1111)^(3*1111) = (4^3 * 1111^3)^1111 = 64^1111 * 1111^3333`
Vì `81 > 64`; `1111^4444>1111^3333`
`=> 3333^4444 > 4444^3333`
`7,`
`A = 2 + 2^2 + 2^3 + ... + 2^20`
`= (2 + 2^2) + (2^3 + 2^4) + ... + (2^19 + 2^20)`
`= 2(1 + 2) + 2^3 (1 + 2) + .... + 2^19(1 + 2)`
`= (2 + 2^3 + ... + 2^19)(1 + 2)`
`= 3*(2 + 2^3 + ... + 2^19)`
Vì \(3\cdot\left(2+2^3+...+2^{19}\right)\text{ }⋮\text{ }3\)
`=> A \vdots 3`
Vậy, `A \vdots 3.`