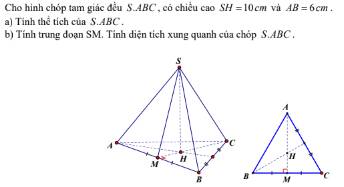
a) Xét tam giác ABC đều có đường cao AM ta có:
\(BC=AB\Rightarrow BM=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác AMB ta có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AM=\sqrt{AB^2-BM^2}\)
\(\Rightarrow AM=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
Diện tích đáy của hình chóp là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AM=\dfrac{1}{2}\cdot3\sqrt{3}\cdot6=9\sqrt{3}\left(cm^2\right)\)
Thể tích của hình chóp là:
\(S_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SH=\dfrac{1}{3}\cdot9\sqrt{3}\cdot10=30\sqrt{3}\left(cm^3\right)\)
b) Do H là giao điểm của hai đường trung tuyến (của tam giác đáy ABC) nên H là trọng tâm của tam giác ABC
\(\Rightarrow HM=\dfrac{1}{3}AM=\dfrac{1}{3}\cdot3\sqrt{3}=\sqrt{3}\left(cm\right)\)
Mà SH là đường cao nên SH⊥MH
Áp dụng định lý Py-ta-go vào tam giác SHM (vuông tại H) ta có:
\(\Rightarrow SM^2=MH^2+SH^2\)
\(\Rightarrow SM=\sqrt{SH^2+MH^2}\)
\(\Rightarrow SM=\sqrt{10^2+\left(\sqrt{3}\right)^2}=\sqrt{103}\left(cm\right)\)
Diện tích xung quanh của hình chóp là:
\(S_{xq}=SM\cdot\dfrac{AB+AC+BC}{2}\)
\(\Rightarrow S_{xq}=\sqrt{103}\cdot\dfrac{6+6+6}{2}=9\sqrt{103}\left(cm^2\right)\)