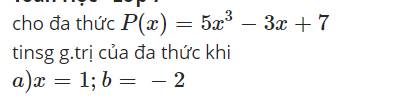\(P\left(x\right)=5x^3-3x+7\)
\(+,\) Với \(x=1\), ta được:
\(P\left(1\right)=5\cdot1^3-3\cdot1+7\)
\(=5-3+7\)
\(=9\)
\(+,\) Với \(x=-2\), ta được:
\(P\left(-2\right)=5\cdot\left(-2\right)^3-3\cdot\left(-2\right)+7\)
\(=5\cdot\left(-8\right)+6+7\)
\(=-40+13\)
\(=-27\)
\(Toru\)
Đa thức \(P\left(x\right)\) có \(b\) đâu nhỉ bạn? Bạn xem lại đề nhé!
\(P\left(x\right)=5x^3-3x+7\)
a) Thay x=-1
=> \(P\left(-1\right)=5.\left(-1\right)^3-3.\left(-1\right)+7\)
\(\Rightarrow P\left(-1\right)=-5+3+7=5\)
b) Thay x=-2
=> \(P\left(-2\right)=5.\left(-2\right)^3-3.\left(-2\right)+7\)
\(\Rightarrow P\left(-2\right)=-40+6+7=-27\)