Question

Answer 1

Bài 2

a) Do AD ⊥ AB (gt)

BC ⊥ AB (gt)

⇒ AD // BC

b) Do AD // BE (cmt)

⇒ ∠ADE = ∠BCD = 118⁰ (đồng vị)

Ta có:

∠BCF + ∠BCD = 180⁰ (kề bù)

⇒ ∠BCF = 180⁰ - ∠BCD

= 180⁰ - 118⁰

= 62⁰

Answer 2

Bài 1

 Ta có:

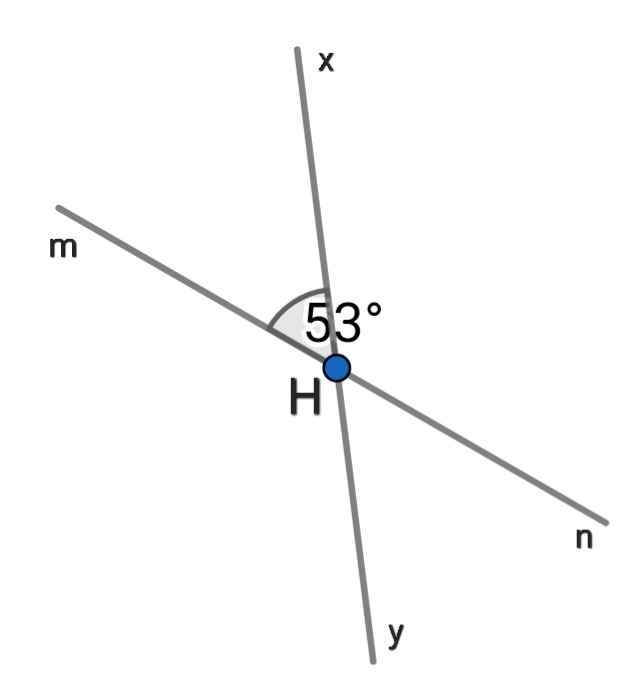
∠nHy = ∠mHx = 53⁰ (đối đỉnh)

∠mHy + ∠mHx = 180⁰ (kề bù)

⇒ ∠mHy = 180⁰ - ∠mHx

= 180⁰ - 53⁰

= 127⁰

⇒ ∠nHx = ∠mHy = 127⁰ (đối đỉnh)

Answer 3

Bài 1

 Ta có:

∠nHy = ∠mHx = 53⁰ (đối đỉnh)

∠mHy + ∠mHx = 180⁰ (kề bù)

⇒ ∠mHy = 180⁰ - ∠mHx

= 180⁰ - 53⁰

= 127⁰

⇒ ∠nHx = ∠mHy = 127⁰ (đối đỉnh)

Bài 2

a) Do AD ⊥ AB (gt)

BC ⊥ AB (gt)

⇒ AD // BC

b) Do AD // BE (cmt)

⇒ ∠ADE = ∠BCD = 118⁰ (đồng vị)

Ta có:

∠BCF + ∠BCD = 180⁰ (kề bù)

⇒ ∠BCF = 180⁰ - ∠BCD

= 180⁰ - 118⁰

= 62⁰