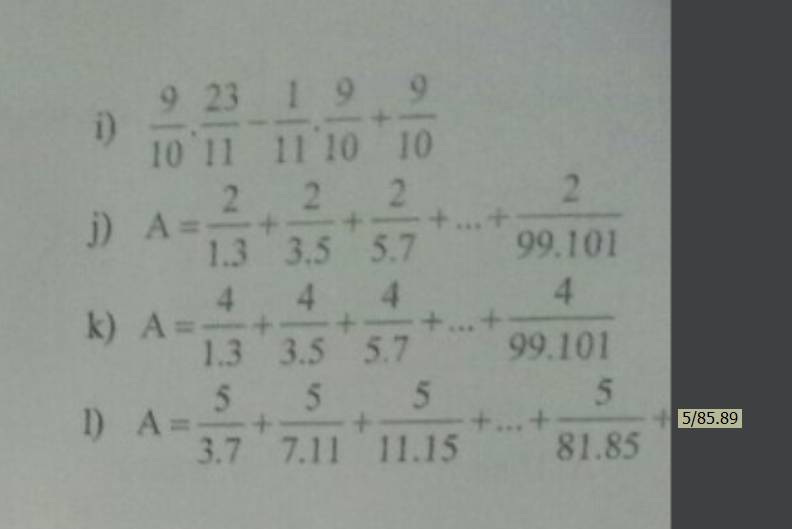i) \(\dfrac{9}{10}.\dfrac{23}{11}-\dfrac{1}{11}.\dfrac{9}{10}+\dfrac{9}{10}\)
\(=\dfrac{9}{10}.\left(\dfrac{23}{11}-\dfrac{1}{11}+1\right)\)
\(=\dfrac{9}{10}.3\)
\(=\dfrac{27}{10}\)
j) \(A=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(=1-\dfrac{1}{101}\)
\(=\dfrac{100}{101}\)
k) \(A=\dfrac{4}{1.3}+\dfrac{4}{3.5}+\dfrac{4}{5.7}+...+\dfrac{4}{99.101}\)
\(=2.\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\right)\)
\(=2.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=2.\left(1-\dfrac{1}{101}\right)\)
\(=2.\dfrac{100}{101}\)
\(=\dfrac{200}{101}\)
l) \(A=\dfrac{5}{3.7}+\dfrac{5}{7.11}+\dfrac{5}{11.15}+...+\dfrac{5}{81.85}+\dfrac{5}{85.89}\)
\(=\dfrac{5}{2}.\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{85}-\dfrac{1}{89}\right)\)
\(=\dfrac{5}{2}.\left(\dfrac{1}{3}-\dfrac{1}{89}\right)\)
\(=\dfrac{5}{2}.\dfrac{86}{267}\)
\(=\dfrac{215}{267}\)
i)\(\dfrac{9}{10}\).\(\dfrac{23}{11}\) -\(\dfrac{1}{11}\) .\(\dfrac{9}{10}\) +\(\dfrac{9}{10}\)
=\(\dfrac{9}{10}\) \(\left(\dfrac{23}{11}-\dfrac{1}{11}\right)\) +\(\dfrac{9}{10}\)
=\(\dfrac{9}{10}\) .2+\(\dfrac{9}{10}\) =\(\dfrac{9}{10}\) (2+1)=\(\dfrac{9}{10}\) .3=\(\dfrac{27}{10}\)
j)A=\(\dfrac{2}{1.3}\) +\(\dfrac{2}{3.5}\) +...+\(\dfrac{2}{99.101}\)
A=1-\(\dfrac{1}{3}\) +\(\dfrac{1}{3}\) -\(\dfrac{1}{5}\) +...+\(\dfrac{1}{99}\) -\(\dfrac{1}{101}\)
A=1-\(\dfrac{1}{101}\) =\(\dfrac{100}{101}\)
k)A=\(\dfrac{4}{1.3}\) +\(\dfrac{4}{3.5}\) +...+\(\dfrac{4}{99.101}\)
A.\(\dfrac{1}{2}\)=\(\dfrac{2}{1.3}\)+\(\dfrac{2}{3.5}\)+...+\(\dfrac{2}{99.101}\)
A.\(\dfrac{1}{2}\)=1-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}\)-\(\dfrac{1}{5}\) +...+\(\dfrac{1}{99}\) -\(\dfrac{1}{101}\)
A.\(\dfrac{1}{2}\)=1-\(\dfrac{1}{101}\)=\(\dfrac{100}{101}\)
A=\(\dfrac{100}{101}\) :2=\(\dfrac{50}{101}\)
l)A=\(\dfrac{5}{3.7}\) +\(\dfrac{5}{7.11}\) +...+\(\dfrac{5}{81.85}\)
\(\dfrac{4}{5}\).A=\(\dfrac{4}{3.7}\) +\(\dfrac{4}{7.11}\) +...+\(\dfrac{4}{81.85}\)
\(\dfrac{4}{5}\).A=\(\dfrac{1}{3}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{11}\)+...+\(\dfrac{1}{81}\)-\(\dfrac{1}{85}\)
\(\dfrac{4}{5}\).A=\(\dfrac{1}{3}\)-\(\dfrac{1}{85}\)=\(\dfrac{88}{225}\)
A=\(\dfrac{88}{225}\):\(\dfrac{4}{5}\)=\(\dfrac{22}{45}\)