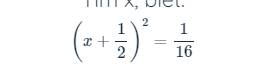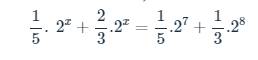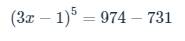\(a>\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)
\(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{4}^2=\left(-\dfrac{1}{4}\right)^2\)
\(x+\dfrac{1}{2}=\dfrac{1}{4}=-\dfrac{1}{4}\)
\(+>x+\dfrac{1}{2}=\dfrac{1}{4}\)
\(\Rightarrow\)\(x=-\dfrac{1}{4}\)
\(+>x+\dfrac{1}{2}=-\dfrac{1}{4}\)
\(\Rightarrow x=-\dfrac{3}{4}\)
\(\Rightarrow x\in\left\{-\dfrac{1}{4};-\dfrac{3}{4}\right\}\)
\(b>\dfrac{1}{5}.2^x+\dfrac{2}{3}.2^x=\dfrac{1}{5}.2^7+\dfrac{1}{3}.2^8\)
\(\dfrac{1}{5}.2^x+\dfrac{2}{3}.2^x=\dfrac{1}{5}.2^7+\dfrac{1}{3}.2.2^7\)
\(\dfrac{1}{5}.2^x+\dfrac{2}{3}.2^x=\dfrac{1}{5}.2^7+\dfrac{2}{3}.2^7\)
\(2^x\left(\dfrac{1}{5}+\dfrac{2}{3}\right)=2^7\left(\dfrac{1}{5}+\dfrac{2}{3}\right)\)
\(\Rightarrow2^x=2^7\)
\(\Rightarrow x=7\)
\(c>\left(3x-1\right)^5=974-731\)
\(\left(3x-1\right)^5=3^5\)
\(\Rightarrow3x-1=3\)
\(3x=3+1=4\)
\(x=\dfrac{4}{3}\)
`#3107.101107`
`(x + 1/2)^2 = 1/16`
`=> (x + 1/2)^2 = (+-1/4)^2`
`=>`\(\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{1}{4}\\x+\dfrac{1}{2}=-\dfrac{1}{4}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{1}{4}-\dfrac{1}{2}\\x=-\dfrac{1}{4}-\dfrac{1}{2}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{3}{4}\end{matrix}\right.\)
Vậy, `x \in {-1/4; -3/4}`
_____
`1/5*2^x + 2/3*2^x = 1/5*2^7 + 1/3*2^8`
`=> (1/5 + 2/3)*2^x = 2^7 * (1/5 + 1/3*2)`
`=> 13/15*2^x = 2^7 * 13/15`
`=> 13/15*2^x - 2^7 * 13/15 = 0`
`=> 13/15*(2^x - 2^7) = 0`
`=> 2^x - 2^7 = 0`
`=> 2^x = 2^7`
`=> x = 7`
Vậy, `x = 7`
_____
`(3x - 1)^5 = 974 - 731`
`=> (3x - 1)^5 = 243`
`=> (3x - 1)^5 = 3^5`
`=> 3x - 1 = 3`
`=> 3x = 3 + 1`
`=> 3x = 4`
`=> x = 4/3`
Vậy, `x = 4/3.`