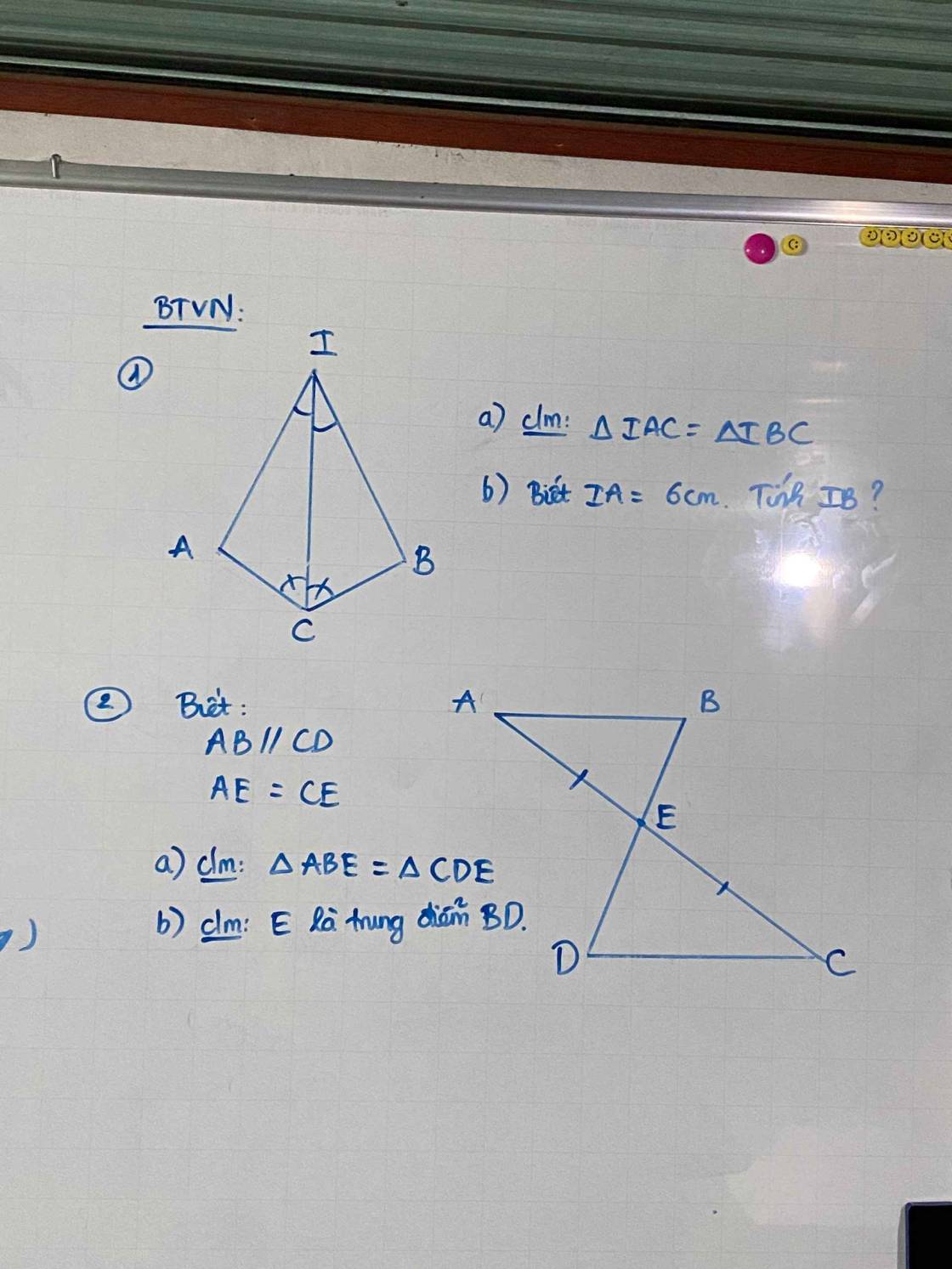
1)
a) Xét ΔIAC và ΔIBC ta có:
\(\widehat{AIC}=\widehat{CIB}\left(gt\right)\)
\(\widehat{ACI}=\widehat{BCI}\left(gt\right)\)
\(IC\) là cạnh chung
\(\Rightarrow\Delta IAC=\Delta IBC\left(g.c.g\right)\)
b) Do \(\Delta IAC=\Delta IBC\left(cmt\right)\)
\(\Rightarrow IA=IB\)
\(\Rightarrow IB=6\left(cm\right)\)
2)
a) Do AB//CD
\(\Rightarrow\widehat{EAB}=\widehat{ECD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{EBA}=\widehat{EDC}\left(so.le.trong\right)\)
Xét ΔABE và ΔCDE ta có:
\(\widehat{EAB}=\widehat{ECD}\left(so.le.trong\right)\)
\(\widehat{EBA}=\widehat{EDC}\left(so.le.trong\right)\)
\(AE=CE\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\)
b) Do \(\Delta ABE=\Delta CDE\left(cmt\right)\)
\(\Rightarrow BE=DE\)
Nên E là trung điểm của BD