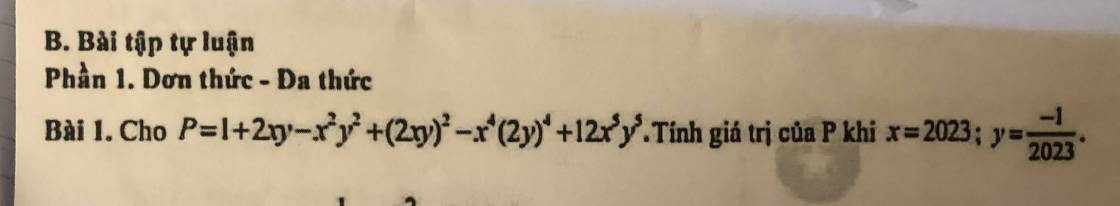\(P=1+2xy-x^2y^2+(2xy)^2-x^4(2y)^4+12x^5y^5\\=1+2xy-x^2y^2+4x^2y^2-16x^4y^4+12x^5y^5\\=12x^5y^5-16x^4y^4+3x^2y^2+2xy+1\\=12\cdot(xy)^5-16\cdot(xy)^4+3\cdot(xy)^2+2\cdot xy+1\)
Ta có: \(x=2023;y=\dfrac{-1}{2023}\)
\(\Leftrightarrow xy=2023\cdot\left(\dfrac{-1}{2023}\right)=-1\)
Thay \(xy=-1\) vào \(P\), ta được:
\(=12\cdot\left(-1\right)^5-16\cdot\left(-1\right)^4+3\cdot\left(-1\right)^2+2\cdot\left(-1\right)+1\)
\(=12\cdot\left(-1\right)-16\cdot1+3\cdot1-2+1\)
\(=-12-16+3-2+1\)
\(=-28+1+1\)
\(=-26\)
Vậy \(P=-26\) khi \(x=2023;y=\dfrac{-1}{2023}\).
#\(Toru\)
Đúng 1
Bình luận (0)
