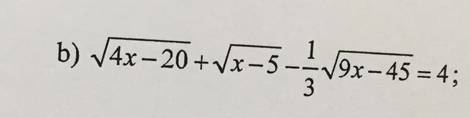\(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\left(dk:x\ge5\right)\\ \Leftrightarrow\sqrt{4\left(x-5\right)}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9\left(x-5\right)}=4\)
\(\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\\ \Leftrightarrow\sqrt{x-5}\left(2+1-1\right)=4\\ \Leftrightarrow2\sqrt{x-5}=4\\ \Leftrightarrow\sqrt{x-5}=2\\ \Leftrightarrow\left|x-5\right|=4\\ \Leftrightarrow x-5=4\\ \Leftrightarrow x=9\left(tmdk\right)\)
Vậy \(S=\left\{9\right\}\)
\(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\left(đk:x\ge5\right)\)
\(< =>\sqrt{4\left(x-5\right)}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9\left(x-5\right)}=4\\ < =>2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\\ < =>3\sqrt{x-5}-\sqrt{x-5}=4\\ < =>2\sqrt{x-5}=4\\ < =>\sqrt{x-5}=2\\ < =>x-5=4\\ < =>x=9\left(tm\right)\)