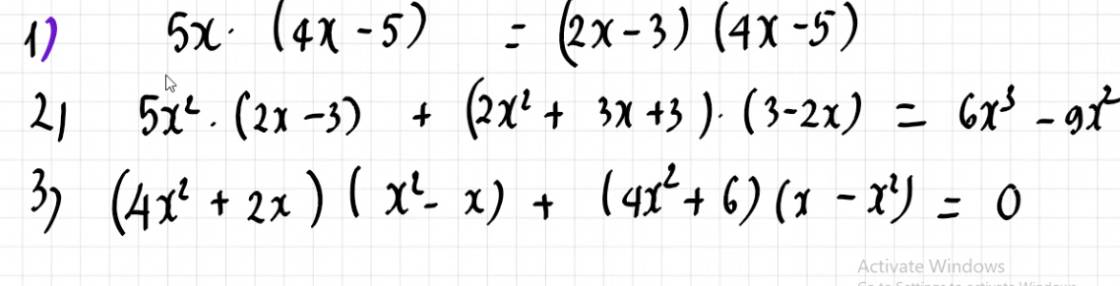\(1) 5x \cdot (4x-5) = (2x-3)(4x-5)\)
\(\Leftrightarrow5x\cdot\left(4x-5\right)-\left(2x-3\right)\left(4x-5\right)=0\)
\(\Leftrightarrow\left(4x-5\right)\left(5x-2x+3\right)=0\)
\(\Leftrightarrow\left(4x-5\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-5=0\\3x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-1\end{matrix}\right.\)
\(---\)
\(2)5x^2\cdot (2x-3)+(2x^2+3x+3)\cdot(3-2x)=6x^3-9x^2\)
\(\Leftrightarrow5x^2\cdot\left(2x-3\right)-\left(2x^2+3x+3\right)\left(2x-3\right)-6x^3+9x^2=0\)
\(\Leftrightarrow\left(2x-3\right)\left[5x^2-\left(2x^2+3x+3\right)\right]-3x^2\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(5x^2-2x^2-3x-3-3x^2\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(-3x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\-3x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-1\end{matrix}\right.\)
\(---\)
\(3)\) \((4x^2+2x)(x^2-x)+(4x^2+6)(x-x^2)=0\)
\(\Leftrightarrow\left(4x^2+2x\right)\left(x^2-x\right)-\left(4x^2+6\right)\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x^2-x\right)\left[4x^2+2x-\left(4x^2+6\right)\right]\)
\(\Leftrightarrow x\left(x-1\right)\left(2x-6\right)=0\)
\(\Leftrightarrow2x\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=3\end{matrix}\right.\)
Vậy: ...
#\(Toru\)