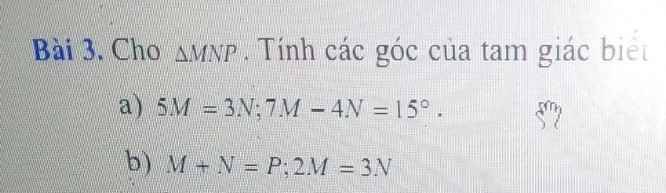a: Đặt \(a=\widehat{M};b=\widehat{N};c=\widehat{P}\)
Ta có: 5M=3N
=>\(5a=3b\)
=>\(\dfrac{a}{3}=\dfrac{b}{5}\)
7M-4N=15
=>7a-4b=15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{7a-4b}{7\cdot3-4\cdot5}=\dfrac{15}{1}=15\)
=>\(a=45;b=75\)
=>\(\widehat{M}=45^0;\widehat{N}=75^0\)
Xét ΔMNP có \(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
=>\(\widehat{P}+75^0+45^0=180^0\)
=>\(\widehat{P}=60^0\)
b: Xét ΔMNP có \(\widehat{M}+\widehat{N}=\widehat{P}\)
mà \(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
nên \(\widehat{P}=\dfrac{180^0}{2}=90^0\)
=>\(\widehat{M}+\widehat{N}=90^0\)
=>a+b=90
2M=3N
=>2a=3b
=>\(\dfrac{a}{3}=\dfrac{b}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{2}=\dfrac{a+b}{3+2}=\dfrac{90}{5}=18\)
=>\(a=3\cdot18=54;b=2\cdot18=36\)
=>\(\widehat{M}=54^0;\widehat{N}=36^0\)