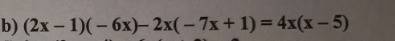b) \(\left(2x-1\right)\left(-6x\right)-2x\left(-7x+1\right)=4x\left(x-5\right)\)
\(\Leftrightarrow-12x^2+6x+14x^2-2x=4x^2-20x\)
\(\Leftrightarrow2x^2+4x=4x^2-20x\)
\(\Leftrightarrow2x^2-4x^2+4x+20x=0\)
\(\Leftrightarrow-2x^2+24x=0\)
\(\Leftrightarrow-2x\left(x-12\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-12=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=12\end{matrix}\right.\)
Vậy: \(S=\left\{0;12\right\}\)
Đúng 1
Bình luận (0)
