a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: ΔBAD=ΔBHD
=>DA=DH
mà DH<DC
nên DA<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
Do đó: ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
ΔBKC cân tại B
mà BI là trung tuyến
nên BI là phân giác của góc ABC
mà BD là phân giáccủa góc ABC
nên B,D,I thẳng hàng
Tk
Giải:
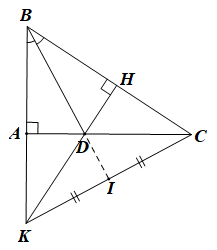
a) Xét DABD và ΔHBD có:
ˆBAD=ˆBHD=90∘
BD là cạnh chung,
ˆABD=ˆHBD(do BD là tia phân giác của ˆABD).
Do đó DABD = ΔHBD (cạnh huyền – góc nhọn).
b) Từ DABD = ΔHBD (câu a) suy ra AD = HD (hai cạnh tương ứng)
Xét DDHC vuông tại H có DC là cạnh huyền nên DC là cạnh lớn nhất
Do đó DC > HD nên DC > AD.
c) Xét DBKC có CA ⊥ BK, KH ⊥ BC và CA cắt KH tại D
Do đó D là trực tâm của DBKC, nên BD ⊥ KC (1)
Gọi J là giao điểm của BD và KC.
Xét DBKJ và DBCJ có:
ˆBJK=ˆBJC=90 \(^o\),
BJ là cạnh chung,
ˆKBJ=ˆCBJ (do BJ là tia phân giác của ˆABD).
Do đó DBKJ = DBCJ (cạnh góc vuông – góc nhọn kề)
Suy ra KJ = CJ (hai cạnh tương ứng)
Hay J là trung điểm của KC.
Mà theo bài I là trung điểm của KC nên I và J trùng nhau.
Do đó ba điểm B, D, I thẳng hàng.
















