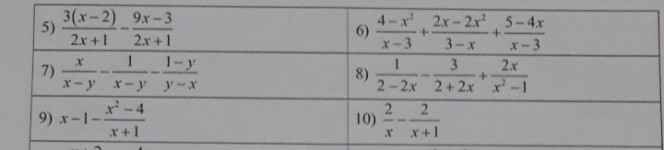
5:
\(=\dfrac{3x-6-9x+3}{2x+1}=\dfrac{-6x-3}{2x+1}=\dfrac{-3\left(2x+1\right)}{2x+1}=-3\)
6: \(\dfrac{4-x^2}{x-3}+\dfrac{2x^2-2x}{x-3}+\dfrac{5-4x}{x-3}\)
\(=\dfrac{4-x^2+2x^2-2x+5-4x}{x-3}=\dfrac{x^2-6x+9}{x-3}\)
\(=\dfrac{\left(x-3\right)^2}{x-3}=x-3\)
7: \(=\dfrac{x-1+1-y}{x-y}=\dfrac{x-y}{x-y}=1\)
8: \(=\dfrac{-1}{2\left(x-1\right)}-\dfrac{3}{2\left(x+1\right)}+\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{-x-1-3x+3+4x}{2\left(x-1\right)\left(x+1\right)}=\dfrac{2}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x^2-1}\)
9: \(=\dfrac{\left(x-1\right)\left(x+1\right)-x^2+4}{x+1}=\dfrac{x^2-1-x^2+4}{x+1}=\dfrac{3}{x+1}\)
10: \(=\dfrac{2x+2-2x}{x\left(x+1\right)}=\dfrac{2}{x\left(x+1\right)}\)
\(\dfrac{3\left(x-2\right)}{2x+1}-\dfrac{9x-3}{2x+1}\\ =\dfrac{3x-6-9x+3}{2x+1}\\ =\dfrac{-6x-3}{2x+1}\\ =\dfrac{-3\left(2x+1\right)}{2x+1}\\ =-3\)
___
\(\dfrac{4-x^2}{x-3}+\dfrac{2x-2x^2}{3-x}+\dfrac{5-4x}{x-3}\\ =\dfrac{4-x^2}{x-3}-\dfrac{2x-2x^2}{x-3}+\dfrac{5-4x}{x-3}\\ =\dfrac{4-x^2-2x+2x^2+5-4x}{x-3}\\ =\dfrac{x^2-6x+9}{x-3}\\ =\dfrac{\left(x-3\right)^2}{x-3}\\ =x-3\)
___
\(\dfrac{x}{x-y}-\dfrac{1}{x-y}-\dfrac{1-y}{y-x}\\ =\dfrac{x}{x-y}-\dfrac{1}{x-y}+\dfrac{1-y}{x-y}\\ =\dfrac{x-1+1-y}{x-y}\\ =\dfrac{x-y}{x-y}\\ =1\)
\(\dfrac{1}{2-2x}-\dfrac{3}{2+2x}+\dfrac{2x}{x^2-1}\\ =\dfrac{1}{2\left(1-x\right)}-\dfrac{3}{2\left(1+x\right)}+\dfrac{3x}{\left(x-1\right)\left(x+1\right)}\\ =-\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{2\left(1+x\right)}+\dfrac{3x}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{-\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{3\left(x-1\right)}{2\left(x+1\right)\left(x-1\right)}+\dfrac{4x}{2\left(x-1\right)\left(x+1\right)}\\ =\dfrac{-x-1-3x+3+4x}{2\left(x+1\right)\left(x-1\right)}\\ =\dfrac{3}{2\left(x+1\right)\left(x-1\right)}\\ =\dfrac{1}{x^2-1}\)
__
\(x-1-\dfrac{x^2-4}{x+1}\\ =\dfrac{x\left(x+1\right)}{x+1}-\dfrac{x+1}{x+1}-\dfrac{x^2-4}{x+1}\\ =\dfrac{x^2+x-x-1-x^2+4}{x+1}\\ =\dfrac{3}{x+1}\)
__
\(\dfrac{2}{x}-\dfrac{2}{x+1}\\ =\dfrac{2\left(x+1\right)}{x\left(x+1\right)}-\dfrac{2x}{x\left(x+1\right)}\\ =\dfrac{2x+2-2x}{x\left(x+1\right)}\\ =\dfrac{2}{x\left(x+1\right)}\)