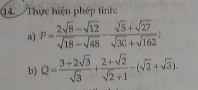\(a)P=\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt[]{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}\)
\(=\dfrac{\sqrt{4.8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}\)
\(=\dfrac{\sqrt{32}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{\sqrt{4}\left(\sqrt{8}-\sqrt{3}\right)}{\sqrt{6}\left(\sqrt{3}-\sqrt{8}\right)}-\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{-2}{\sqrt{6}}-\dfrac{1}{\sqrt{6}}=\dfrac{-3}{\sqrt{6}}\)
\(=\dfrac{\sqrt{6}}{2}\)
\(b)Q=\dfrac{3-2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{\sqrt{2}+1}-\left(\sqrt{2}+\sqrt{3}\right)\)
\(=\dfrac{\sqrt{3}\left(\sqrt{3}-2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\left(\sqrt{2}+\sqrt{3}\right)\)
\(=\sqrt{3}-2+\sqrt{2}-\left(\sqrt{2}+\sqrt{3}\right)\)
\(=-2\)