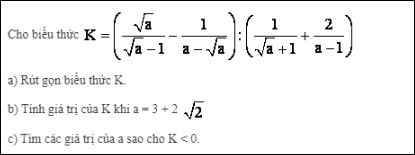a) ĐKXĐ: \(\left\{{}\begin{matrix}a\ge0\\a\ne1\end{matrix}\right.\)
K=\(\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)
\(=\left[\dfrac{a}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\left[\dfrac{\left(\sqrt{a}-1\right)+2}{a-1}\right]\)
\(=\dfrac{\sqrt{a}+1}{\sqrt{a}}\):\(\dfrac{1}{\sqrt{a}-1}\)
=\(\dfrac{a-1}{\sqrt{a}}\)
b) Khi a=3+\(2\sqrt{2}\), ta có:
K=\(\dfrac{2+2\sqrt{2}}{\sqrt{\left(\sqrt{2}+1\right)^2}}=\dfrac{\sqrt{2}\left(\sqrt{2+1}\right)}{\sqrt{2}+1}=\sqrt{2}\)
c) Vì\(\sqrt{a}>0\) nên để K<0 thì a-1<0 =>a<1
Đúng 1
Bình luận (0)