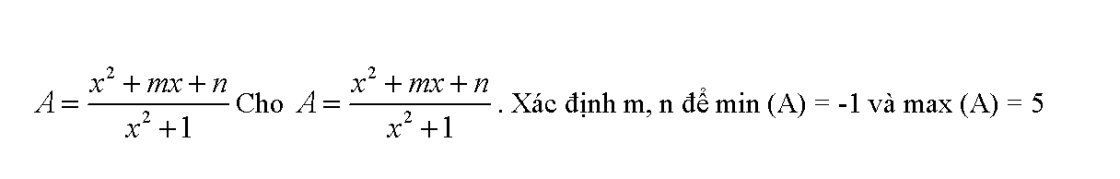Ta có:
\(A=\dfrac{x^2+mx+n}{x^2+1}\)\(\Leftrightarrow A\left(x^2+1\right)=x^2+mx+n\)
\(\Leftrightarrow\left(A-1\right)x^2-mx+A-n=0\left(1\right)\)
Với \(A\ne1\), để pt \(\left(1\right)\) có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow m^2-4\left(A-1\right)\left(A-n\right)\ge0\)
Do \(A_{min}=-1;A_{max}=5\) nên \(\left[{}\begin{matrix}A=1\\A=5\end{matrix}\right.\) tm \(m^2-4\left(A-1\right)\left(A-n\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4\left(-1-1\right)\left(-1-n\right)=0\\m^2-4\left(5-1\right)\left(5-n\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=4\sqrt{2}\\m=-4\sqrt{2}\end{matrix}\right.\\n=3\end{matrix}\right.\)