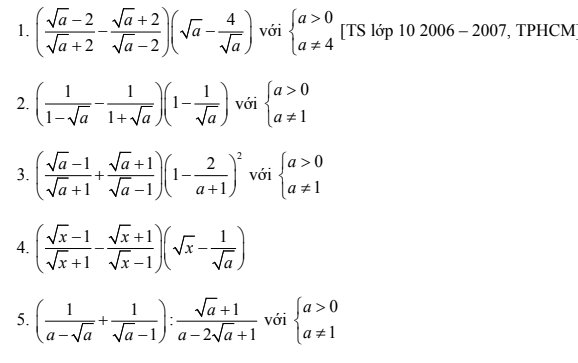1
\(=\left(\dfrac{\left(\sqrt{a}-2\right)^2}{a-4}-\dfrac{\left(\sqrt{a}+2\right)^2}{a-4}\right)\left(\dfrac{a-4}{\sqrt{a}}\right)\\ =\left(\dfrac{a-4\sqrt{a}+4-a-4\sqrt{a}-4}{a-4}\right)\left(\dfrac{a-4}{\sqrt{a}}\right)\\ =\dfrac{-8\sqrt{a}\left(a-4\right)}{\left(a-4\right).\sqrt{a}}=-8\)
2
\(=\left(\dfrac{1+\sqrt{a}}{1-a}-\dfrac{1-\sqrt{a}}{1-a}\right)\left(\dfrac{\sqrt{a}-1}{\sqrt{a}}\right)\\ =\left(\dfrac{1+\sqrt{a}-1+\sqrt{a}}{1-a}\right)\left(\dfrac{\sqrt{a}-1}{\sqrt{a}}\right)\\ =\dfrac{2\sqrt{a}\left(\sqrt{a}-1\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right).\sqrt{a}}\\ =-\dfrac{2\sqrt{a}\left(1-\sqrt{a}\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right).\sqrt{a}}\\ =-\dfrac{2}{1+\sqrt{a}}\)
3
\(=\left(\dfrac{\left(\sqrt{a}-1\right)^2}{a-1}+\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}\right)\left(\dfrac{a+1-2}{a+1}\right)^2\\ =(\dfrac{a-2\sqrt{a}+1+a+2\sqrt{a}+1}{a-1})\left(\dfrac{a-1}{a+1}\right)^2\\ =\left(\dfrac{2\left(a+1\right)}{a-1}\right).\dfrac{\left(a-1\right)^2}{\left(a+1\right)^2}\\ =\dfrac{2\left(a+1\right)\left(a-1\right)^2}{\left(a-1\right)\left(a+1\right)^2}\\ =\dfrac{2\left(a-1\right)}{a+1}\\ =\dfrac{2a-2}{a+1}\)
4 ĐK: \(x\ne1;a>0\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)^2}{x-1}-\dfrac{\left(\sqrt{x}+1\right)^2}{x-1}\right)\left(\dfrac{\sqrt{xa}-1}{\sqrt{a}}\right)\\ =(\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{x-1})\left(\dfrac{\sqrt{xa}-1}{\sqrt{a}}\right)\\ =\dfrac{-4\sqrt{x}\left(\sqrt{xa}-1\right)}{\sqrt{a}\left(x-1\right)}\)(Đâu ra 2 biến trong rút gọn là thấy sai rồi: )
5
\(=\left(\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)^2}\right)\\ =\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}.\left(\dfrac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+1\right)}\right)\\ =\dfrac{\left(1+\sqrt{a}\right)\left(\sqrt{a}-1\right)^2}{\sqrt{a}\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ =\dfrac{\sqrt{a}-1}{\sqrt{a}}\)