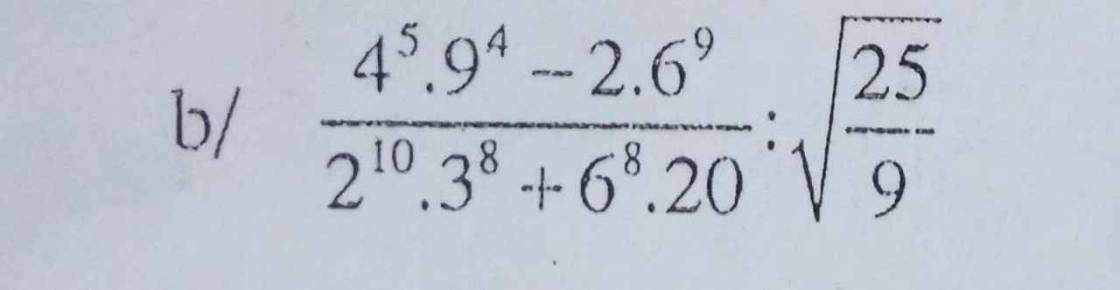`@` `\text {Ans}`
`\downarrow`
`b,`
\(\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}\div\sqrt{\dfrac{25}{9}}\)
\(=\dfrac{2^{10}\cdot3^8-2\cdot2^9\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot20}\div\dfrac{5}{3}\)
\(=\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot2^2\cdot5}\div\dfrac{5}{3}\)
\(=\dfrac{2^{10}\cdot3^8\cdot\left(1-3\right)}{2^{10}\cdot3^8\cdot6}\div\dfrac{5}{3}\)
\(=-\dfrac{2}{6}\div\dfrac{5}{3}\)
\(=-\dfrac{1}{3}\cdot\dfrac{3}{5}=-\dfrac{1}{5}\)
\(=\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}:\dfrac{5}{3}\)
\(=\dfrac{2^{10}\cdot3^8\cdot\left(1-3\right)}{2^{10}\cdot3^8\cdot6}\cdot\dfrac{3}{5}=\dfrac{-2}{6}\cdot\dfrac{3}{5}=-\dfrac{1}{5}\)