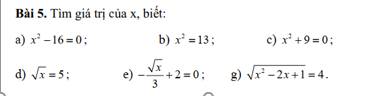\(a,x^2-16=0\Leftrightarrow x^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
Vậy \(S=\left\{4;-4\right\}\)
\(b,x^2=13\) \(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{13}\\x=-\sqrt{13}\end{matrix}\right.\)
Vậy \(S=\left\{-\sqrt{13};\sqrt{13}\right\}\)
\(c,x^2+9=0\Leftrightarrow x^2=-9\)
Vậy \(S=\varnothing\)
\(d,\sqrt{x}=5\Leftrightarrow x=5^2\Leftrightarrow x=25\)
Vậy \(S=\left\{25\right\}\)
\(e,-\dfrac{\sqrt{x}}{3}+2=0\Leftrightarrow-\dfrac{\sqrt{x}}{3}=-2\Leftrightarrow\dfrac{\sqrt{x}}{3}=2\Leftrightarrow\sqrt{x}=6\Leftrightarrow x=6^2\Leftrightarrow x=36\)
Vậy \(S=\left\{36\right\}\)
\(g,\sqrt{x^2-2x+1}=4\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}=4\)
\(\Leftrightarrow\left|x-1\right|=4\)
\(\left|x-1\right|=\left\{{}\begin{matrix}x-1khix\ge1\\-x+1khix< 1\end{matrix}\right.\)
Với \(x\ge1\Leftrightarrow x-1=4\Leftrightarrow x=5\left(tm\right)\)
Với \(x< 1\Leftrightarrow-x+1=4\Leftrightarrow-x=3\Leftrightarrow x=-3\left(tm\right)\)
Vậy \(S=\left\{-3;5\right\}\)