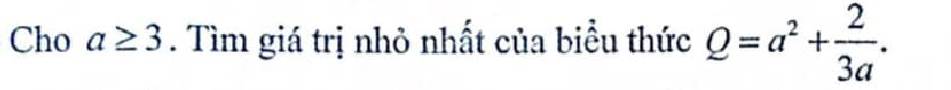Question

Answer 1

Q' = 2a + \(\dfrac{2}{3}\) 

Q = 2a + \(\dfrac{2}{3}\) 

\(\Rightarrow a=\dfrac{-1}{3}\) 

Vì a \(\ge3\) nên a = \(\dfrac{-1}{3}\) không phù hợp

Vậy ta lấy giá trị nhỏ nhất là 3

Thay a = 3 vào giá trị biểu thức của Q = a² +\(\dfrac{2}{3a}\) , ta có:

  Q = \(3^2+\dfrac{2}{3.3}\) 

\(Q=9+\dfrac{2}{9}\) \(\approx9.22\) 

Vậy ....

 

 

Answer 2

Ta có: \(Q=a^2+\dfrac{2}{3a}\ge3^2+\dfrac{2}{3.3}=9+\dfrac{2}{9}=\dfrac{83}{9}\)(do \(a\ge3\))

\(\Rightarrow Min_Q=\dfrac{83}{9}\)

Dấu "=" xảy ra khi \(a=3\)

Vậy \(Min_P=\dfrac{83}{9}\) khi \(a=3\)