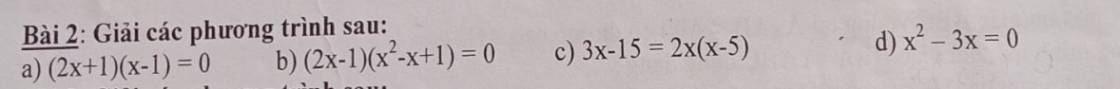a) \(\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow2x+1=0\) hoặc \(x-1=0\)
*) \(2x+1=0\)
\(\Leftrightarrow2x=-1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
*) \(x-1=0\)
\(\Leftrightarrow x=1\)
Vậy \(S=\left\{-\dfrac{1}{2};1\right\}\)
b) \(\left(2x-1\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow2x-1=0\) hoặc \(x^2-x+1=0\)
*) \(2x-1=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
*) \(x^2-x+1=0\)
Ta có:
\(x^2-x+1=x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi \(x\in R\)
Do đó: \(x^2-x+1=0\) là vô lý
Vậy \(S=\left\{\dfrac{1}{2}\right\}\)
c) \(3x-15=2x\left(x-5\right)\)
\(\Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(3-2x\right)=0\)
\(\Leftrightarrow x-5=0\) hoặc \(3-2x=0\)
*) \(x-5=0\)
\(\Leftrightarrow x=5\)
*) \(3-2x=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=\dfrac{3}{2}\)
Vậy \(S=\left\{\dfrac{3}{2};5\right\}\)
d) \(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(x-3=0\)
*) \(x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(S=\left\{0;3\right\}\)