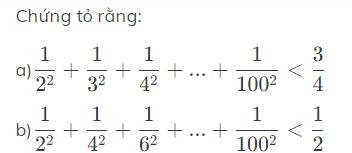a: \(\frac{1}{3^2}<\frac{1}{2\cdot3}=\frac12-\frac13\)
\(\frac{1}{4^2}<\frac{1}{3\cdot4}=\frac13-\frac14\)
...
\(\frac{1}{100^2}<\frac{1}{99\cdot100}=\frac{1}{99}-\frac{1}{100}\)
Do đó: \(\frac{1}{3^2}+\frac{1}{4^2}+\cdots+\frac{1}{100^2}<\frac12-\frac13+\frac13-\frac14+\cdots+\frac{1}{99}-\frac{1}{100}=\frac12-\frac{1}{100}<\frac12\)
=>\(\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{100^2}<\frac14+\frac12=\frac34\)
b: Đặt \(A=\frac{1}{2^2}+\frac{1}{4^2}+\cdots+\frac{1}{100^2}\)
\(=\frac{1}{2^2}\left(1+\frac{1}{2^2}+\cdots+\frac{1}{50^2}\right)\)
Ta có: \(\frac{1}{2^2}<\frac{1}{1\cdot2}=1-\frac12\)
\(\frac{1}{3^2}<\frac{1}{2\cdot3}=\frac12-\frac13\)
...
\(\frac{1}{50^2}<\frac{1}{49\cdot50}=\frac{1}{49}-\frac{1}{50}\)
Do đó: \(\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{50^2}<1-\frac12+\frac12-\frac13+\cdots+\frac{1}{49}-\frac{1}{50}\)
=>\(\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{50^2}<1-\frac{1}{50}<1\)
=>\(1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{50^2}<1+1=2\)
=>\(\frac{1}{2^2}\left(1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{50^2}\right)<\frac14\cdot2=\frac12\)
=>\(A<\frac12\)