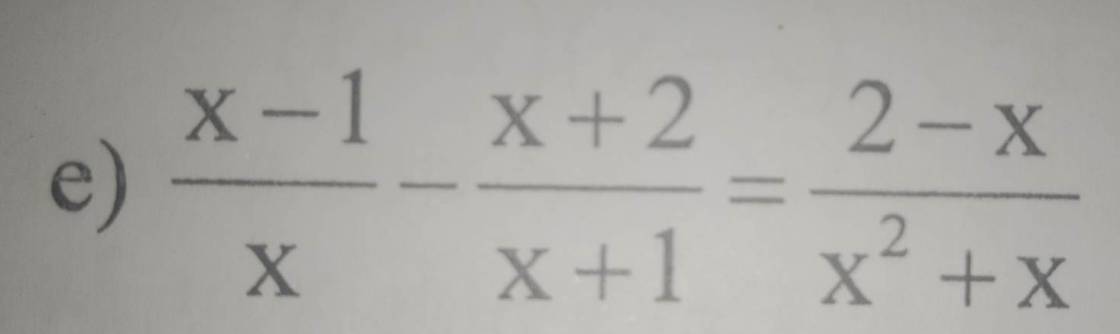e)\(\dfrac{x-1}{x}-\dfrac{x+2}{x+1}=\dfrac{2-x}{x^2+x}\)
\(ĐKXĐ:x\ne0;x\ne-1\)
\(\dfrac{x-1}{x}-\dfrac{x+2}{x+1}=\dfrac{2-x}{x^2+1}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}-\dfrac{\left(x+2\right)x}{\left(x+1\right)x}=\dfrac{2-x}{x^2+x}\)
\(\Rightarrow x^2+x-x-1-x^2-2x=2-x\)
\(\Leftrightarrow x^2-x^2+x-x-2x+x=2+1\)
\(\Leftrightarrow-x=3\)
\(\Leftrightarrow x=-3\left(TMĐKXĐ\right)\)
Vậy phương trình có tập nghiệm là: \(S=\left\{-3\right\}\)
Đúng 1
Bình luận (0)
