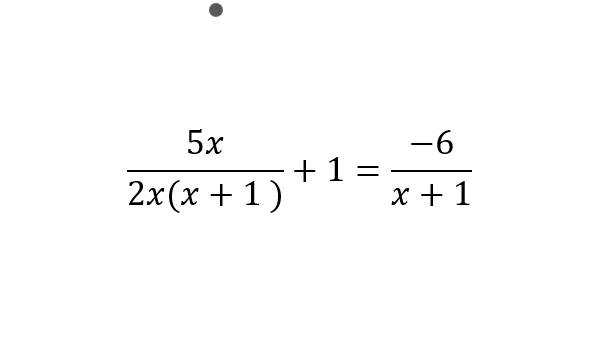ĐKXĐ: x ≠ 0 và x ≠ -1
Phương trình tương đương:
5x + 2x(x + 1) = -6.2x
⇔ 5x + 2x² + 2x + 12x = 0
⇔ 2x² + 19x = 0
⇔ x(2x + 19) = 0
⇔ x = 0 (loại) hoặc 2x + 19 = 0
*) 2x + 19 = 0
⇔ 2x = -19
⇔ x = -19/2 (nhận)
Vậy S = {-19/2}
\(\dfrac{5x}{2x\left(x+1\right)}+1=\dfrac{-6}{x+1}\text{ĐKXĐ:}x\ne0;x\ne-1\)
\(\Leftrightarrow\dfrac{5x}{2x\left(x+1\right)}+\dfrac{2x\left(x+1\right)}{2x\left(x+1\right)}=\dfrac{-6.2x}{2x\left(x+1\right)}\)
\(\Rightarrow5x+2x^2+2x=-12x\)
\(\Leftrightarrow2x^2+7x=-12x\)
\(\Leftrightarrow2x^2+7x+12x=0\)
\(\Leftrightarrow2x^2+19x=0\)
\(\Leftrightarrow x\left(2x+19\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x+19=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=-19\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(\text{loại}\right)\\x=\dfrac{-19}{2}\left(\text{nhận}\right)\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{\dfrac{-19}{2}\right\}\)