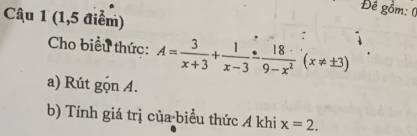a)
\(A=\dfrac{3}{x+3}+\dfrac{1}{x-3}-\dfrac{18}{9-x^2}\\ =\dfrac{3}{x+3}+\dfrac{1}{x-3}+\dfrac{18}{x^2-9}\\ =\dfrac{3\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}+\dfrac{18}{\left(x-3\right)\left(x+3\right)}\\ =\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}\\ =\dfrac{4x+12}{\left(x-3\right)\left(x+3\right)}\\ =\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\\ =\dfrac{4}{x-3}\)
b)
với x=2(tmđk) thì
\(\dfrac{4}{2-3}=\dfrac{4}{-1}=-4\)
a: \(=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4x+12}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\)
b: Khi x=2 thì \(A=\dfrac{4}{2-3}=-4\)