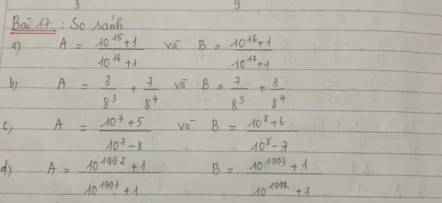a: \(10A=\dfrac{10^{16}+10}{10^{16}+1}=1+\dfrac{9}{10^{16}+1}\)
\(10B=\dfrac{10^{17}+10}{10^{17}+1}=1+\dfrac{9}{10^{17}+1}\)
mà 10^16+1<10^17+1
nên 10A>10B
=>A>B
c: \(A=\dfrac{10^7-8+13}{10^7-8}=1+\dfrac{13}{10^7-8}\)
\(B=\dfrac{10^8-7+13}{10^8-7}=1+\dfrac{13}{10^8-7}\)
mà 10^7-8<10^8-7
nên A>B
d: \(\dfrac{1}{10}A=\dfrac{10^{1992}+1}{10^{1992}+10}=1+\dfrac{-9}{10^{1992}+10}\)
\(\dfrac{1}{10}B=\dfrac{10^{1993}+1}{10^{1993}+10}=1+\dfrac{-9}{10^{1993}+10}\)
mà 10^1992+10<10^1993+10
nên A<B
Đúng 0
Bình luận (0)
