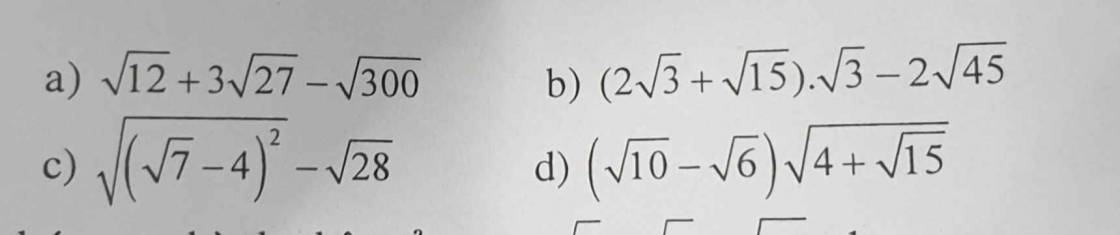\(\sqrt{12}+3\sqrt{27}-\sqrt{300}=2\sqrt{3}+9\sqrt{3}-10\sqrt{3}=\sqrt{3}\)
\(\left(2\sqrt{3}+\sqrt{15}\right)\sqrt{3}-2\sqrt{45}=2.3+\sqrt{45}-6\sqrt{5}=6+3\sqrt{5}-6\sqrt{5}=6-3\sqrt{5}\)
\(\sqrt{\left(\sqrt{7}-4\right)^2}-\sqrt{28}=\left|\sqrt{7}-4\right|-2\sqrt{7}=4-\sqrt{7}-2\sqrt{7}=4-3\sqrt{7}\)
\(\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8+2\sqrt{15}}=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
Lời giải:
a.
$\sqrt{12}+3\sqrt{27}-\sqrt{300}=\sqrt{2^2.3}+3\sqrt{3^2.3}-\sqrt{10^2.3}$
$=2\sqrt{3}+3.3\sqrt{3}-10\sqrt{3}=2\sqrt{3}+9\sqrt{3}-10\sqrt{3}$
$=\sqrt{3}(2+9-10)=\sqrt{3}$
b.
$(2\sqrt{3}+\sqrt{15})\sqrt{3}-2\sqrt{45}$
$=2\sqrt{3}.\sqrt{3}+\sqrt{45}-2\sqrt{45}$
$=2.3-\sqrt{45}=6-\sqrt{3^2.5}=6-3\sqrt{5}$
c.
$\sqrt{(\sqrt{7}-4)^2}=-\sqrt{28}=|\sqrt{7}-4|-\sqrt{2^2.7}$
$=4-\sqrt{7}-2\sqrt{7}=4-3\sqrt{7}$
d.
$(\sqrt{10}-\sqrt{6})\sqrt{4+\sqrt{15}}$
$=(\sqrt{5}-\sqrt{3})\sqrt{8+2\sqrt{15}}$
$=(\sqrt{5}-\sqrt{3})\sqrt{(\sqrt{5}+\sqrt{3})^2}$
$=(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})=5-3=2$