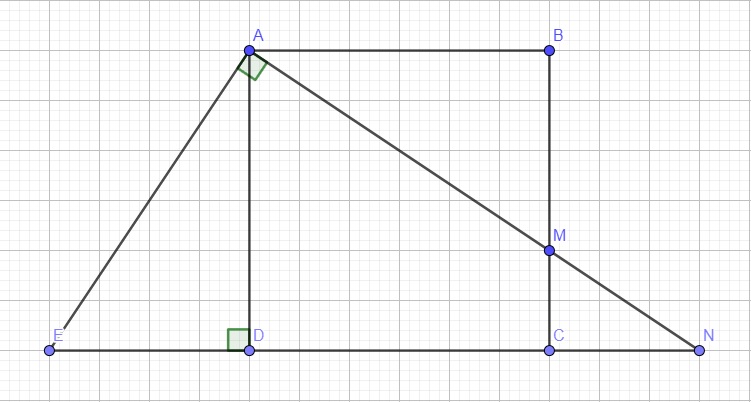
Qua A kẻ đường thẳng vuông góc AM cắt CD kéo dài tại E
\(\Rightarrow\widehat{DEA}=\widehat{BAM}\) (cùng phụ \(\widehat{DAM}\))
Xét hai tam giác DAE và BAM có:
\(\left\{{}\begin{matrix}\widehat{DEA}=\widehat{BAM}\\AD=AB\\\widehat{ADE}=\widehat{ABM}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta DAE=\Delta BAM\left(g.c.g\right)\)
\(\Rightarrow AM=AE\)
Áp dụng hệ thức lượng trong tam giác vuông AEN với đường cao AD:
\(\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AN^2}\)
\(\Leftrightarrow\dfrac{1}{AD^2}=\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\)
Vậy \(P=\dfrac{1}{AD^2}\)
Đúng 0
Bình luận (0)
